開爾文函式

開爾文函式(Kelvin function)有兩大類函式，兩大類分別由實部和虛部構成。實部分別對應ber(x)、ker(x)，虛部分別對應為bei(x)、kei(x)。

基本介紹

• 中文名：開爾文函式
• 外文名：Kelvin function
• 學科：數理科學
• 分類：第一類、第二類

簡介

開爾文函式有兩類。第一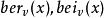類；第二類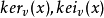

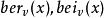
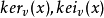
第一類開爾文函式

ber（x）

對於整數n，ber_n（x）有系列擴展

其中Γ（z）是伽馬函式。特殊情況ber₀（x），通常表示為ber（x），具有系列擴張

和漸近系列

其中

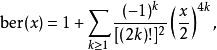
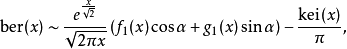
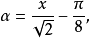
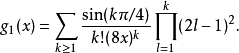
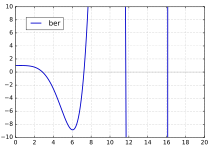圖1.x在0~20的ber(x)函式曲線

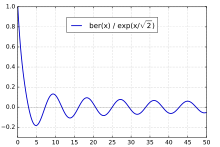圖2.x在1~50之間函式曲線

bei（x）

對於整數n，bei_n（x）具有系列擴展

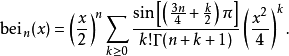
特殊情況bei₀（x），通常表示為bei（x），具有序列擴張

和漸近系列

其中α， ，和 被定義為ber（x）。

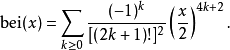
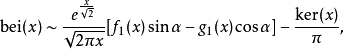
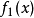
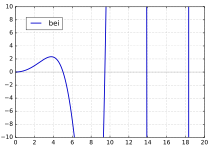圖3.x在0~20之間的函式曲線

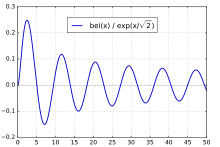圖4.x在0~50之間的函式曲線

第二類開爾文函式

ker（x）

特殊情況ker₀（x），通常表示為ker（x），具有序列擴展

和漸近級數

其中

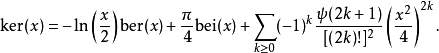
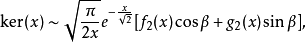
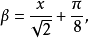
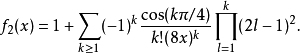
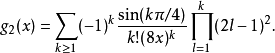
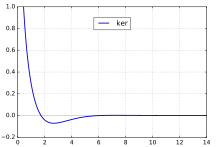圖5.x在0~14之間的函式曲線

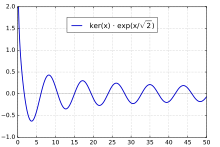圖6.x在0~50之間的函式曲線

kei（x）

通常表示為kei（x）的特例kei₀（x）具有系列擴張

和漸近級數

其中β，f₂（x）和g₂（x）被定義為ker（x）。

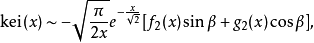
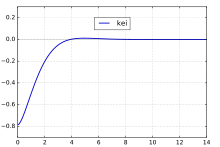圖7.x在0~14之間的函式曲線

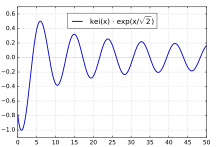圖8.x在0~50之間的函式曲線