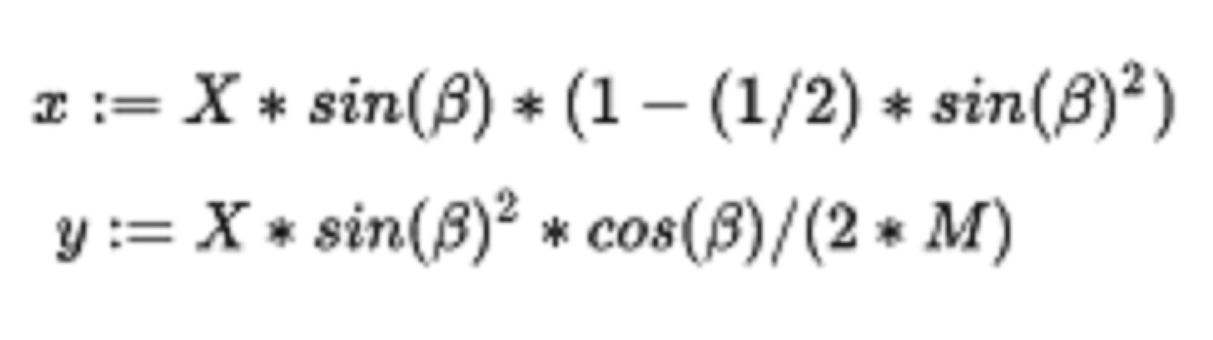船隻在湖面經過時,在後面會激起一道V形的波。開爾文男爵最先對船波進行數學研究,因此稱為開爾文船波。
基本介紹
- 中文名:開爾文船波
- 外文名:Kelvin ship wave
- 領域:力學
- 形狀:V型波
- 發現者:開爾文男爵
- 相似名詞:表面波
簡介,多鞍點函式積分,開爾文駐相法,
簡介
船隻在湖面經過時,在後面會激起一道V形的波。開爾文男爵最先對船波進行數學研究,因此稱為開爾文船波。
船波動形狀和福祿數Fr有密切關係 開爾文傳播的數學模擬
開爾文傳播的數學模擬
 開爾文傳播的數學模擬
開爾文傳播的數學模擬
其中g為重力常數,V是船速,l是船的長度。
令船的長度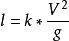
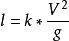
則

對於長度大而速度低的輪船,Fr數小,開爾文船波主要是長波,其波前與速度矢量的夾角比較小。
而小快艇,長度小,速度高,Fr 數大,開爾文船波則以短波長的水波為主,而波前則與速度數量成較大的夾角
開爾文船波動研究,對於船舶的設計有重要意義,因為船舶的馬力,有一部分消耗在激起船波。利用Fr數與速度成正比,與長度的平方根成反比的規律,可以利用小的模型,縮小船長M2倍,同時縮小速度M倍,可以在實驗室中模擬海上巨舟。
多鞍點函式積分
當船隻以速度V駛過深水湖面,波形的幅度在相對於船隻為靜止的極坐標中由下列公式表示

其中 ,g為重力常數,l為船的長度。
,g為重力常數,l為船的長度。

上列K函式是下列多鞍點積分的正數部分:

此核函式是一個多鞍點函式。求其極點,

解之θ,得

因此

這就是凱爾文船波的V型波包線的夾角,最早由凱爾文男爵發現,而且角度與船速無關.至於波紋本身則與船速矢量的夾角為
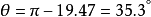
開爾文駐相法
開爾文船波積分必須通過數值積分計算。開爾文男爵根據被積分函式在積分區間內劇烈震盪的特點,提出了駐相法(Method of Stationary Phase)。
原理:當被積分函式劇烈震盪時,除了在極點外,震盪的被積分函式正負相抵消,因此可以將此被積分函式在極點的值作為整個積分的近似,駐相法乃是拉普拉斯方法的推廣。
被積分函式如下

兩個極點是:

令

開爾文船波的波峰,由下列兩個參數方程式描述