基本介紹
- 中文名:長度收縮效應
- 外文名:Length contract effect
- 別稱:尺縮效應
- 提出時間:1892年
- 領域:狹義相對論
簡史
長度收縮效應


推導和說明
 尺縮效應運動測量
尺縮效應運動測量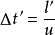
 尺縮效應地面測量
尺縮效應地面測量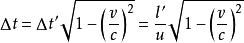
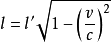


 尺縮效應運動測量
尺縮效應運動測量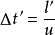
 尺縮效應地面測量
尺縮效應地面測量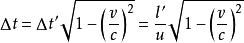
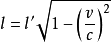
長度收縮效應(Length contract effect),又稱尺縮效應,是相對論性效應之一。一根靜止長桿的長度可以用標準尺子進行測量。對於沿桿子的方向作勻速直線運動的另一根桿子...
鐘慢、尺縮、時間倒流,都可以用聲音試驗做出類似的結果。在物理上被稱為都卜勒效應。如果一個鐘,以0.5倍聲速從原點遠去,我們會聽到什麼現象呢?一秒鐘時,它距離...
這種情況被叫做長度收縮效應,或尺縮效應。這個效應顯示了空間的相對性。對於同一個物體,在相對於該物體運動的參考系中,沿運動方向測量它的長度,所得的結果要比在...
代表作品 由“長度收縮”效應引發的猜想、微科普、中國天文快訊 [8] 專業 物理學 職位 微科普網主編、中國天文快訊主編 [6] 目錄...
這種情況被叫做長度收縮效應,或尺縮效應。這個效應顯示了空間的相對性,對於同一個物體,在相對於該物體運動的參考系中,沿運動方向測量它的長度,所得的結果要比在...
長度和時間間隔的測量與觀測者的運動無關,物質間相互作用的傳遞是瞬時到達的;...在狹義相對論中,給出了長度收縮效應和時間膨脹效應,從而得出質點的質量是速度的...
在長度收縮效應中,物體在運動方向上收縮的現象是由“測量”得到的,考慮的是光同時從物體兩端發出的情況;而特勒爾效應考慮的是從高速運動的物體發出的光線同時到達...
三、 長度收縮效應四、 速度變換法則§8-3 狹義相對論動力學一、 質速關係和相對論動力學基本方程二、 質能關係三、 能量-動量關係...
二、長度收縮效應75三、時間延緩效應77第四節狹義相對論動力學基礎77一、相對論中的動量和質量77二、相對論動能78三、質能關係式79四、相對論能量與動量的關係79...
第五節 修改引力透鏡效應 第六節 修改運動時間膨脹效應 第七節 修改長度收縮效應 第八節 修改引力時間延遲效應 第九節 修改行星近日點進動公式 第十節 修改引力...
