錢德拉篩子

錢德拉篩子，森德拉姆的正方形篩子的第一橫行是首項為4，相鄰兩數之差為3的等差數列：4，7，10，…(可以一直寫下去，永遠寫不到頭)．第二行，第三行，……以後的任何一行也都是等差數列，只不過相鄰兩數之差逐漸變大，分別是5，7，9，11，13，…，而且都是奇數。

基本介紹

  • 中文名：錢德拉篩子
  • 時間：1934年
  • 學者：森德拉姆
  • 領域：數論領域
時間,數學原理,

時間

1934年，來自東印度(今孟加拉國)的普通學者——森德拉姆，在數論領域中取得了一個輝煌成就。

數學原理

我們先畫一張正方形表格，表格中橫行與縱列的地位是完全一樣的．在數學上，稱為“對稱矩陣”。
4
7
10
13
16
19
22
25
……
7
12
17
22
27
32
37
42
……
10
17
24
31
38
45
52
59
……
13
22
31
40
49
58
67
76

16
27
38
49
60
71
82
93
……
19
32
45
58
71
84
97
110
……
……
……
……
……
……
……
……
……
……
森德拉姆的正方形篩子的第一橫行是首項為4，相鄰兩數之差為3的等差數列：4，7，10，…(可以一直寫下去，永遠寫不到頭)．第二行，第三行，……以後的任何一行也都是等差數列，只不過相鄰兩數之差逐漸變大，分別是5，7，9，11，13，…，而且都是奇數。
（1）如果某個自然數N出現在表中，那么2N+1肯定不是質數，如果N在表中不出現，那么2N+1肯定是質數。
（2）矩陣的第n行，第m列的通項為：N=2nm+m+n(m≥1,n≥1,m,n是正整數)
錢德拉篩子
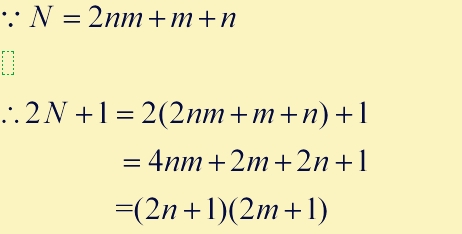
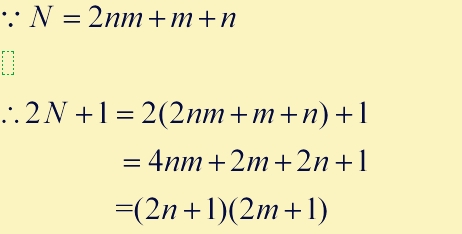
若N在表中第n行、第m列出現，則（2N+1）可表示為右側的：
顯然（2N+1）是一個合數，這是兩個大於或等於3的奇數的乘積。
設2n+1=a,2m+1=b,
N應該出現在矩陣的:n=（a-1）/2行，m=（b-1）/2列。
例如，2N+1=ab=133=7×19，
2N= 133-1=132
N =132÷2=66
n=(7-1)/2=3(行)m=(19-1)/2=9(列)
則N=66出現在第3行，第9列。
(根據乘法交換律，9行3列也有)
66=2×3×9+3+9

相關詞條

熱門詞條

聯絡我們