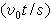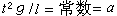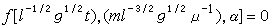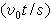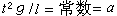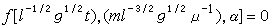人們通過定義各種物理量定性和定量地描述物理現象,確定物理系統所處的狀態。任一物理量的定義給出被定義量與有關量之間的關係。物理量之間的有規律聯繫還通過描述自然規律的各種定律表示出來。因此當一個單位制的基本量確定後,其他的物理量就可以通過既定的關係或定律,定義為用基本量表示的導出量,並通過代數式表示為基本量的冪次乘積。例如力學中常用的MKS和CGS單位制,基本量都是長度L、質量M和時間T,而速度、加速度和力等力學量就是分別通過它們的定義式和牛頓運動定律定義的導出量。而國際單位制(SI)有七個基本量:長度L、質量M、時間T、電流I、溫度Θ、物質的量N和光強度J。
量綱將一個物理量Q表示為基本量的冪次之積(忽略其矢量或張量特性,以及包括正負號在內的所有數字因素)的表達式
, (1)
稱為該物理量對選定的一組基本量的量綱積或量綱。冪次指數α、β、γ、δ、ε、ζ和η稱為量綱指數。七個基本量的量綱分別為L、M、T、I、Θ、N和J,稱為該單位制的基本量綱。下表列出了寫成式 (1)形式的一些物理量的量綱,其中1表示無量綱。
由於選取的基本量不相同,同一個物理量在不同的單位制里的量綱可以互不相同。這在電磁學中是常有的。例如高斯單位制中的基本量是長度、質量和時間,而電磁學的MKSA制中的基本量是長度、質量、時間和電流。因此,在高斯單位制里電量q的量綱dim
,而在MKSA制中,電量的量綱dimq=IT。
物理量的量綱積(1) 可以用來作不同單位制之間的單位換算。如力學中常用的MKS制和CGS制的基本量相同,但基本量的單位不同:MKS制的基本量單位為米(m)、千克(kg)和秒(s);CGS制的基本量單位為厘米(cm)、克(g)和秒(s)。則由力的量綱dimF=LMT可知,從CGS制變換到MKS制時, 因基本量L和M的單位分別增為10和10倍,故MKS制中力的單位牛頓應為 CGS制中力的單位達因的10倍。
物理量之間的一定組合,使其量綱積內基本量的量綱指數均為零,稱為無量綱積或無量綱物理量,有時也稱為量綱為1的量。例如應變dl/l的量綱dim(dl/l)=LL=1;雷諾數Re=vlρ/μ,其中v、ρ、μ分別是流體的速率、密度和粘滯率;l是物體或容器的特徵線度,顯然有 dimRe=LT·L·ML·MLT=MLT=1
無量綱量的量綱為1,所以它的數值與所選用的單位制無關,用純數表示。
量綱分析任一合理構成的物理方程中的各項,都具有相同的量綱。如自由落體距離
(2)
其中v0是初速,g是重力加速度,t是時間。確實,方程(2)中的三項的量綱都是L,這樣的方程稱為具有量綱一致性。顯然,量綱一致的方程的形式,不會因基本量的單位不同而改變。
量綱分析的基本定理是Pi定理(π定理),它表述為:若有一量綱一致的方程,其中包含由r個獨立的基本量所定義的n個物理量,則此方程必可導致一個包含有(n-r)個獨立的無量綱乘積之間的關係式。這就是說,設有一個包含n個變數A的量綱一致的方程為 F(A1,A2,…,An)=0, (3)
必可得一個包含k=n-r個獨立的無量綱積的關係式 f(π1,π2,…πk)=0。 (4)
以式(2)為例,根據Pi定理,導致一個聯繫兩個獨立的無量綱積
和
之間的關係式:
。這兩個無量綱積是獨立的,因為它們中的一個,不能由另一個導出:由變數s、v0、g、t可以組成的其他無量綱積都可以由這兩個無量綱積導出。在量綱分析中把具有這種性質的一組無量綱積稱為完全系。
下面以單擺振盪為例,說明量綱分析的套用。在單擺振盪這一力學現象中,描述振盪規律的運動方程中應包含以下物理量:振盪周期t,擺桿長l,重力加速度g和擺角α。故與式(3)相對應有 F(t,l,g,α)=0。 (5)
則根據Pi定理,k=2,即應有兩個獨立的無量綱積。注意到式(5)中四個物理量的量綱分別為dimt呏T,diml呏L,dimg呏LT,dimα呏1,則兩個無量綱積應為:π1=gt/l,π2=α。故與式(4)相應有
。 (6)
式(6)可改寫為
或
(7)
其中只有 嗘(α)是一個未確定的函式。故可得到結論,當擺角α一定時,振盪周期與擺桿長的平方根成正比。
若只討論小α角的情況,顯然α角不再是重要的變數。由三個量l、g和t只能組成一個無量綱積tg/l,故得
或 。 (8)
正確的力學計算表明,常數 a=2π。這就是說,簡單的量綱分析可以導致一個正確的常數乘因子的解。
由單擺振盪的量綱分析還可看出,擺的質量m對振盪周期沒有影響,因為與振盪過程有關的物理量的量綱式中,無一是包含質量量綱M的。這就是說,不可能在力學量t、l、g和m的基礎上,建立一個量綱一致的方程。
上列分析中,完全忽略了空氣的粘滯阻力和軸承內的摩擦阻力對振盪過程的影響,若只討論空氣粘滯阻力引起的振盪衰減,在運動方程中將多出一個物理量空氣的粘滯率μ。如前所述μ的量綱為MLT,則根據Pi定理,無量綱積的關係式為
。 (9)
套用量綱分析於單擺振盪的例子表明,從研究一個過程中各個物理量的量綱及其間的關係,可以推導出必須加於這些物理量的某些限制,這是量綱分析的主要用途。這種方法既普遍又簡單,但它不能給出完全確定的解。在一些較為複雜的包含很多物理量的過程中,例如在流體動力學和換熱換質理論中遇到的一定形狀的物體在連續媒質中運動所受到的阻力,或物體運動過程中放出的熱量等問題,有的不能從數學上嚴格求解,有的甚至列不出確切描述這一過程的方程。量綱分析得出的變數之間必須遵守的關係式,可以減少問題的不確定因素。在此基礎上,套用相似性理論,通過模型試驗,確定關係式的一般函式形式,有很大的實際意義。
參考書目
E.Buckingham,Phys. Rev., Vol.4,No.4,p.32,1914.
E.Isaacson and M.Isaacson,Dimensional Methods in Engineering and Physics, Arnold, London, 1975.