量子閘

量子閘，即量子門，在量子計算和特別是量子線路的計算模型裡面，一個量子門 (或量子邏輯門)是一個基本的，操作一個小數量量子比特的量子線路 。它是量子線路的基礎，就像傳統邏輯門跟一般數字線路之間的關係。

與多數傳統邏輯門不同，量子邏輯門是可逆的。然而，傳統的計算可以只使用可逆的門表示.舉例來說，可逆的Toffoli門可以實做所有的布爾函式。這個門有一個直接等同的量子門，也因此代表量子線路可以模擬所有傳統線路的操作。

量子邏輯門使用酉矩陣表示。就像常見的邏輯門一般是針對一個或兩個比特進行操作，常見的量子門也是針對一個或兩個量子比特進行操作。這也代表這一些量子門可以以2×2或者4×4的酉矩陣表示。

基本介紹

• 中文名：量子閘
• 外文名：Quantum logic gate
• 解釋：操作一個小數量量子位元量子線路
• 簡介：量子線路的基礎
• 表示方式：使用矩陣表示

簡介

量子閘，即量子門，在量子計算和特別是量子線路的計算模型裡面，一個量子門(或量子邏輯門)是一個基本的，操作一個小數量量子比特的量子線路。它是量子線路的基礎，就像傳統邏輯門跟一般數字線路之間的關係。

與多數傳統邏輯門不同，量子邏輯門是可逆的。然而，傳統的計算可以只使用可逆的門表示.舉例來說，可逆的Toffoli門可以實做所有的布爾函式。這個門有一個直接等同的量子門，也因此代表量子線路可以模擬所有傳統線路的操作。

量子邏輯門使用酉矩陣表示。就像常見的邏輯門一般是針對一個或兩個比特進行操作，常見的量子門也是針對一個或兩個量子比特進行操作。這也代表這一些量子門可以以2×2或者4×4的酉矩陣表示。

量子線路

量子線路或沿用古典稱呼而稱作量子電路，是在抽象概念下，對於量子資訊儲存單元（例如量子比特）進行操作的線路。組成包括了於量子資訊儲存單元、線路（時間線），以及各種邏輯門；最後常需要量子測量將結果讀取出來。

實際上在以物理系統實踐量子計算機時，需要透過轉換，成為實際上的操作方式。例如在核磁共振量子電腦，就需要轉換成射頻，或者射頻搭配梯度磁場的磁振脈衝序列。

萬能量子門

較不正式地說，一個萬能量子門的集合，是一個任何量子線路均可以用這一些門實做出來的集合。也就是說，任何其他的單位操作均可以從這個集合組合出一個有限長度的序列來表示。 技術上來說，因為可能的量子門數目是不可數的，而從有限大的集合取出的有限長度的序列則是可數的，所以不可能達成。為了解決這個問題，我們只要求這一個有限大小的集合可以組合出近似任何量子運算的序列。Solovay–Kitaev theorem保證這一件事情可以有效達成。

一個簡單的，操作兩個量子比特的門，的萬能量子門集合是一個阿達馬門，一個相位偏移門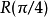 ，和一個受控非門.

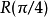
只有單一個量子門的萬能量子門集合可以用一個操作三個量子比特的Deutsch門建構出來，Deutsch門它的操作如下：

在傳統邏輯線路裡面的萬用運算元Toffoli門可以被簡化成一個Deutsch門， ，因此代表著所有傳統邏輯線路的操作均可以由量子電腦模擬。

參見

• 泡利矩陣