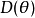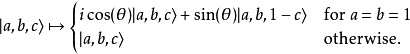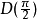在量子計算，特別是量子線路的計算模型裡面，一個量子門 (Quantum gate，或量子邏輯門)是一個基本的，操作一個小數量量子比特的量子線路 。它是量子線路的基礎，就像傳統邏輯門跟一般數字線路之間的關係。
與多數傳統邏輯門不同，量子邏輯門是可逆的。 然而，傳統的計算可以只使用可逆的門表示· 舉例來說，可逆的Toffoli門 可以實做所有的布爾函式。 這個門有一個直接等同的量子門，也因此代表量子線路可以模擬所有傳統線路的操作。
量子邏輯門使用酉矩陣表示。 就像常見的邏輯門一般是針對一個或兩個比特進行操作，常見的量子門也是針對一個或兩個量子比特進行操作。 這也代表這一些量子門可以以2 × 2或者4 × 4的酉矩陣表示。
基本介紹
歷史,基本的量子門,阿達馬門,泡利-X 門,泡利-Y 門,泡利-Z 門,相位偏移門,互換門,Toffoli門,萬能量子門,
歷史
現現有量子門的記號是Barenco et al.發明的，建立在費曼所提出的記號上。
基本的量子門
量子門常使用矩陣表示，操作K個量子比特的門可以用2k x 2k 的酉矩陣表示。 一個門輸入跟輸出的量子比特數量必須要相等。 量子門的操作可以用代表量子門的矩陣與代表量子比特狀態的向量作相乘來表示。
阿達馬門
阿達馬門是只對一個一個量子比特進行操作的門。 這個門將基本狀態 |0> 變成
，並且將 |1> 變成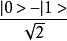
。這個門可以以阿達馬矩陣表示：
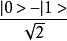
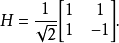
因因為矩陣的每一列正交，因此H 是一個酉矩陣。
泡利-X 門
泡利-X 門操作一個量子比特。 這個門相當於經典的邏輯非門。 它將 |0>換成 |1>並且 |1>換成 |0>。這個門可以用一個 泡利 X 矩陣表示：
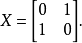
泡利-Y 門
泡利-Y 門操作一個量子比特。這個門可以用一個 泡利 Y 矩陣表示：
泡利-Z 門
泡利-Z 操作一個量子比特。 這個門保留基本狀態 |0>不變,並且將 |1>換成 |-1>。 這個門可以用一個 泡利 Z 矩陣表示：
相位偏移門
相位偏移門是一系列操作單一量子比特的門，它保留基本狀態 |0>並且將 |1>換成 eiθ|1>。
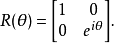
互換門
互換門操作兩個量子比特，可以用以下這個矩陣表示：
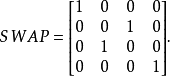
Toffoli門
Toffoli門是一個操作三個量子比特的，對傳統運算比較完備的門。量子的Toffoli門是類同的門，以三個量子比特定義。如果前兩個量子比特是 |1>，則對第三個量子比特進行泡利-X運算，反之則不做操作。這是一個受控門的範例。由於這個門是一個傳統邏輯門的量子模擬，因此它可以用一個真值表來完整表示如下：
Input | Output | ||||
0 | 0 | 0 | 0 | 0 | 0 |
0 | 0 | 1 | 0 | 0 | 1 |
0 | 1 | 0 | 0 | 1 | 0 |
0 | 1 | 1 | 0 | 1 | 1 |
1 | 0 | 0 | 1 | 0 | 0 |
1 | 0 | 1 | 1 | 0 | 1 |
1 | 1 | 0 | 1 | 1 | 1 |
1 | 1 | 1 | 1 | 1 | 0 |
這個門也可以這么形容：它的功能相當於將 |a,b,c> 轉化成了 |a,b,c⊕ab>。（註：⊕為異或運算）
萬能量子門
一個萬能量子門的集合，是一個任何量子線路均可以用這一些門實做出來的集合。也就是說，任何其他的單位操作均可以從這個集合組合出一個有限長度的序列來表示。 技術上來說，因為可能的量子門數目是不可數的，而從有限大的集合取出的有限長度的序列則是可數的，所以不可能達成。為了解決這個問題，我們只要求這一個有限大小的集合可以組合出近似任何量子運算的序列。Solovay–Kitaev theorem保證這一件事情可以有效達成。
一個簡單的，操作兩個量子比特的門，的萬能量子門集合是一個阿達馬門H，一個相位偏移門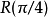
，和一個受控非門。
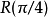
只有單一個量子門的萬能量子門集合可以用一個操作三個量子比特的Deutsch門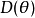
建構出來，Deutsch門它的操作如下：
