研究大量服從量子力學規律、處於平衡態的全同粒子或粒子系統的統計方法。
基本介紹
- 中文名:量子統計法
- 簡介:全同粒子或粒子系統的統計方法
- 釋義:專業名詞
- 涉及學科:物理
源起,算法,
源起
研究大量服從量子力學規律、處於平衡態的全同粒子或粒子系統的統計方法。全同粒子是指互換這類粒子並不導致系統出現新的狀態。全同粒子系統可分兩類,一類由對稱波函式描述的粒子所構成的系統,稱玻色系統。近獨立粒子玻色系統的每一個量子態上占據的粒子數不限,這種粒子遵循的統計稱玻色統計,或稱玻色-愛因斯坦統計,是由S.玻色和A.愛因斯坦在1924年先後提出來的。另一類由反對稱波函式描述的粒子所構成的系統,稱費密系統。這種粒子必須遵循泡利不相容原理,每個量子態上至多只能有一個粒子,它們遵循的統計稱費密統計,或費密-狄喇克統計,是由E.費密和P.A.M.狄喇克在1926年先後提出的。
算法
設近獨立全同粒子組成的系統具有確定的粒子數 N,能量E和體積V,以εi和gi分別表示單粒子的第i個(i=1,2,3,…)能級和對應該能級的量子態數(簡併度)。①對於玻色系統,由於粒子的不可分辨和每個態上占據的粒子數不限,則給定的Ni個粒子分布在gi個量子態的方式數,等於從Ni+gi-1個元素中選取gi-1個元素的組合數

。考慮各能級的結果,就得到對應粒子數分布{Ni}的系統微觀狀態數
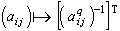
②對於費密系統,Ni個不可分辨的全同粒子分布在gi個狀態上(每個態上至多只能有一個粒子)的可能方式數,就是從 gi個元素中選取 Ni個元素的組合數,應該等於

,則對應粒子數分布{Ni}的系統微觀狀態數

若任一能級 εi上的粒子數Ni均遠小於該能級的量子態數gi,Ni/gi<<1,即絕大多數量子態均未被占據,則可以得到

這就過渡到了玻耳茲曼系統的微觀狀態數。
利用條件
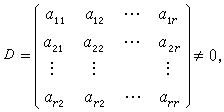
經過計算可得粒子數按能級的最可幾分布為
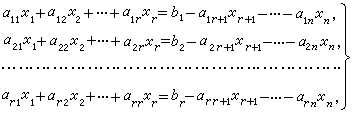
此式分母中的正負號分別對應於費密系統和玻色系統。能級為εp的量子態p上的平均粒子數為

由條件
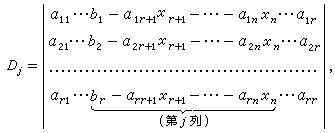
可確定化學勢μ 對T和N 的依賴關係,

是對所有量子態求和。顯然,當

時,費密分布和玻色分布都過渡到玻耳茲曼分布,所以獨立的統計分布只有費密分布和玻色分布兩種。
還可以知道,玻色統計中的化學勢總是負的(μ<0),而光子氣體,由於N不是給定的常數,則μ應等於零。在玻耳茲曼統計中μ也總是負的,且絕對值很大。費密統計中μ可正可負。
在費密和玻色兩種分布中,以T、V、μ為獨立變數的巨熱力勢為:

,
其中Ξ 是巨配分函式(見巨正則系綜)。於是系統的熱力學性質都可根據熱力學公式求得。
