鄰位對換法是全排列生成算法中的其中一種,它的換位是雙向的,通過保存數字的“方向性”來快速得到下一個排列。
基本介紹
- 中文名:鄰位對換法
- 外文名:Ortho transposition method
- 屬性:名詞
- 類別:術語
規則,原理,
規則
設我們要生成n=9的全排列(1,2,3,4,5,6,7,8,9),設定b2b3b4b5b6b7b8b9為我們要求的中介數。
2的方向一定是向左。b2就是從2開始,背向2的方向所有比2小的數字的個數。知道了b2的值之後就可以推 導出b3b4……直到b9的值。
規則如下:
對於每一個大於2的數字i,
如果i為奇數,其方向性決定於bi-1的奇偶性,奇向右、偶向左。
如果i為偶數,其方向性決定於bi-1+ bi-2的奇偶性,同樣是奇向右、偶向左。
當得到方向性後,bi的值就是背向i的方向直到排列邊界這個區間裡比i小的數字的個數。如此就能得到鄰位對 換法的中介數。
舉例
原排列(839647521)生成中介數方法:
如右圖1所示,
2的方向向左,

圖1
背向2的方向中比2小的數字有1個,b2=1
3的方向由b2為奇可以斷定向右,
背向3的方向中比3小的數字有0個,b3=0
4的方向由b2+b3為奇可以斷定向右,
背向4的方向中比4小的數字有1個,b4=1
5的方向由b4為奇可以斷定向右,
背向5的方向中比5小的數字有2個,b5=2
6的方向由b4+b5為奇可以斷定向右,
背向6的方向中比6小的數字有1個,b6=1
7的方向由b6為奇可以斷定向右,
背向7的方向中比7小的數字有3個,b7=3
8的方向由b6+b7為偶可以斷定向左,
背向8的方向中比8小的數字有7個,b8=7
9的方向由b8為奇可以斷定向右,
背向9的方向中比9小的數字有2個,b9=2
從中介數(10121372)得到原排列: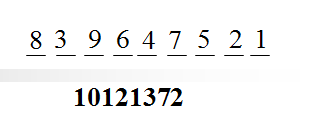
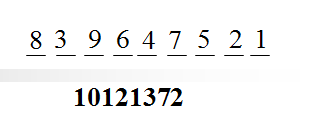
鄰位對換法
9:b8=7奇→9向右b9=2向右第3個空,
8:b6+b7=1+3=4偶→8向左b8=7 向左第8個空
7:b6=1奇→7向右,b7=3 向右第4個空
6:b4+b5=1+2=3奇→6向右,b6=1,向右第2個空
5:b4=1奇→5向右,b5=2,向右第3個空
4:b2+b3=1奇→4向右, b4=1,向右第2個空
3:b2=1奇→3向右, b3=0,向右第1個空
2:b2=1,向左第2個空
總之,如若要從原排列生成下一個排列,首先將原排列按上述方法轉換為中介數,再將中介數加一,得到新中介數,再將新中介數用以上方法換算為下一個排列。
原理
一、算法的原理:
{1, 2, 3, …, n-1, n}的全排列可由{1, 2, 3, …, n-1}的全排列得出。具體做法為針對{1, 2, 3, …, n-1}的任意一個排列{a1, a2, a3, …, an-1},將n插入n個不同的位置得到:
{a1, a2, a3, …, an-1, n},
{a1, a2, a3, …, n, an-1},
……
{a1, a2, n, …, an-2, an-1},
{a1, n, a2, …, an-2, an-1},
{n, a1, a2, …, an-2, an-1}
即可得到{1, 2, 3, …, n-1, n}的全排列。
二、鄰位對換法:
1、 每個數有一個移動方向,向左或向右。如果數x的移動方向上最靠近它的數比它要小,那么x是可移動的。初始時序列為{1, 2, 3, …, n-1, n},方向都為向左。
2、 移動最大數n,直到不能移動為止,每改變一次位置輸出一個序列(此時n在最左邊或最右邊)。
3、 找當前可移動的最大數m。若能找到,移動m,把所有比m大的數的方向置反,返回第2步;若不能找到,算法停止。
舉例:
用sign[]來表示方向,sign[i]表示第i+1大的數的方向。用perm[]來表示序列,以n=4為例。
1、初始狀態
sign:{0, 0, 0, 0}
perm:{1, 2, 3, 4}
移動n=4
perm:{1, 2, 4, 3}
perm:{1, 4, 2, 3}
perm:{4, 1, 2, 3} //能注意到,這4個是在{1, 2, 3}的基礎上添加4得到的排列
2、找到可移動的最大數m=3,移動m,把4的方向置反
sign:{0, 0, 0, 1}
perm:{4, 1, 3, 2}
移動n=4
perm:{1, 4, 3, 2}
perm:{1, 3, 4, 2}
perm:{1, 3, 2, 4} //能注意到,這4個是在{1, 3, 2}的基礎上添加4得到的排列
3、找到可移動的最大數m=3,移動m,把4的方向置反
sign:{0, 0, 0, 0}
perm:{3, 1, 2, 4}
移動n=4
perm:{3, 1, 4, 2}
perm:{3, 4, 1, 2}
perm:{4, 3, 1, 2} //能注意到,這4個是在{3, 1, 2}的基礎上添加4得到的排列
4、 找到可移動的最大數m=2,移動m,把3, 4的方向置反
sign:{0, 0, 1, 1}
perm:{4, 3, 2, 1}
移動n=4
perm:{3, 4, 2, 1}
perm:{3, 2, 4, 1}
perm:{3, 2, 1, 4} //能注意到,這4個是在{3, 2, 1}的基礎上添加4得到的排列
5、 找到可移動的最大數m=3,移動m,把4的方向置反
sign:{0, 0, 1, 0}
perm:{2, 3, 1, 4}
移動n=4
perm:{2, 3, 4, 1}
perm:{2, 4, 3, 1}
perm:{4, 2, 3, 1} //能注意到,這4個是在{2, 3, 1}的基礎上添加4得到的排列
6、 找到可移動的最大數m=3,移動m,把4的方向置反
sign:{0, 0, 1, 1}
perm: {4, 2, 1, 3}
移動n=4
perm: {2, 4, 1, 3}
perm: {2, 1, 4, 3}
perm: {2, 1, 3, 4} //能注意到,這4個是在{2, 1, 3}的基礎上添加4得到的排列
此時發現沒有可移動的數了,算法結束。
三、c語言實現示例:
#include
#define MAXSIZE 100
int orientation[MAXSIZE];
char permData[MAXSIZE];
long count = 0;
void generatePearm(int n) {
int pos;
char temp;
if (permData[0] == ('a' + n - 1)) {
pos = 0;
while(pos < n - 1) {
count++;
//puts(permData);
temp = permData[pos];
permData[pos] = permData[pos+1];
permData[pos+1] = temp;
pos++;
}
count++;
//puts(permData);
} else {
pos = n - 1;
while (pos > 0) {
count++;
//puts(permData);
temp = permData[pos];
permData[pos] = permData[pos-1];
permData[pos-1] = temp;
pos--;
}
count++;
//puts(permData);
}
}
int nCantMove(int n) {
char max = 'a';
int pos = -1, i;
for (i = 1; i < n - 1; i++) {
if (permData[i] < max)
continue;
if ((orientation[permData[i]-'a'] && permData[i] > permData[i+1]) || (!orientation[permData[i]-'a'] && permData[i] > permData[i-1])) {
max = permData[i];
pos = i;
}
}
if ((permData[0] != 'a' + n - 1) && permData[0] > max && permData[0] > permData[1] && orientation[permData[0]-'a']) {
max = permData[0];
pos = 0;
}
if ((permData[n-1] != 'a' + n - 1) && permData[n-1] > max && permData[n-1] > permData[n-2] && !orientation[permData[n-1]-'a']) {
max = permData[n-1];
pos = n - 1;
}
if (max == 'a')
return 0;
if (orientation[max-'a']) {
permData[pos] = permData[pos+1];
permData[pos+1] = max;
} else {
permData[pos] = permData[pos-1];
permData[pos-1] = max;
}
for (i = 0; i < n; i++) {
if (permData[i] > max) {
orientation[permData[i]-'a'] = 1 - orientation[permData[i]-'a'];
}
}
return 1;
}
void nearPosExchGeneratePerm(int n) {
do {
generatePearm(n);
} while (nCantMove(n));
printf("%ld\n", count);
}
int main() {
int n, i;
scanf("%d", &n);
for (i = 0; i < n; i++) {
orientation[i] = 0;
permData[i] = 'a' + i;
}
permData[n] = '\0';
nearPosExchGeneratePerm(n);
return 0;
}

