鄧克利公式

概況

計算振動系統最小固有頻率（即基頻）下界的一個經驗公式，是S.鄧克利於1894年在研究旋轉軸的臨界轉速時從實驗結果中導出的，因而得名。

考慮由連續體（例如梁、板等）和其上n個集中質量組成的系統,fi為不計集中質量時該連續體的基頻,fi為只計第i個集中質量,不計其餘集中質量和連續體質量時單自由度系統的固有頻率，則鄧克利公式為：

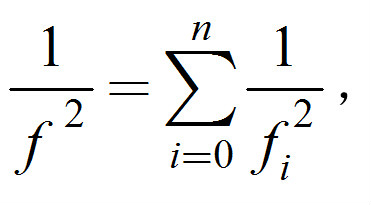
式中f是整個系統的基頻的近似值,它小於準確值。若系統是不計連續體質量的n自由度離散系統,則作為上式的特殊情形，右端求和從1至n。鄧克利公式可用理論加以證明，而且由該公式求出的基頻和實際基頻的相對誤差同實際基頻和第二階固有頻率之比的平方屬於同一量級。

一個如圖 1所示的兩端置於軸承上而跨中有一圓盤(質量為m)的軸的基頻,可將軸簡化為如圖 2所示的跨中有一集中質量的等截面簡支梁。當不計集中質量時，該梁的基頻為：

式中l為梁的長度；A為梁的截面積；EI為梁的彎曲剛度；ρ為梁材料的密度。只計圓盤質量，不計梁的質量時,梁相當一根無質量的彈簧，這個單自由度系統的固有頻率為：

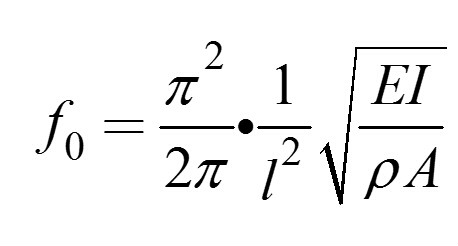
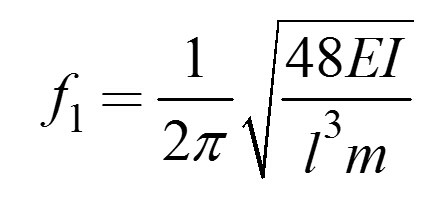
如果圓盤質量和軸的質量相等，即m=ρAl，則

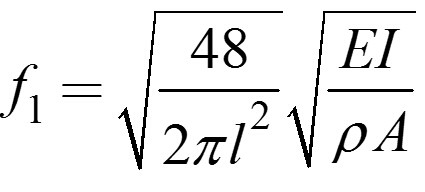
這樣，將f0、f1代入鄧克利公式，得：

而這個梁系的最小固有頻率的準確值為：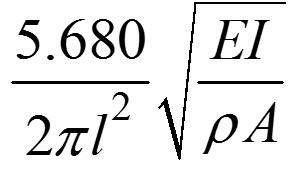

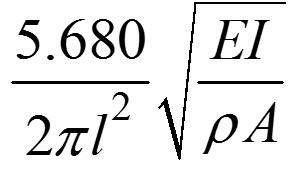
此外，在鄧克利公式的基礎上還可導出精度更高的計算公式。