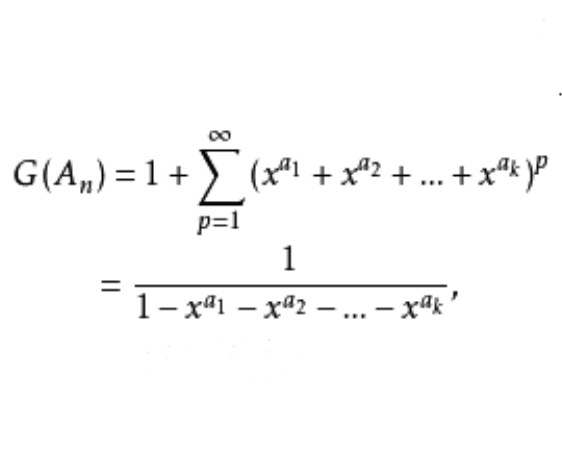郵票排列問題

郵票排列問題(problem of stamp permutation)是一類確定某種排列數的問題，寄信需郵票n分，今用面值為a₁分，a₂分，…，a_k分(a₁<a₂<…a_k≤n)的k種郵票各若干枚，依任意方式依次貼在信封右上角，其面值總和恰為n分，不同的排列方式為不同貼法，求有多少種郵票貼法?這就是郵票排列問題。

基本介紹

• 中文名：郵票排列問題
• 外文名：problem of stamp permutation
• 所屬學科：數學
• 所屬問題：排列組合
• 簡介：一類確定某種排列數的問題

郵票排列問題的解答

郵票排列問題是一類確定某種排列數的問題。

寄信需郵票n分，今用面值為a₁分，a₂分，…，a_k分的k種郵票各若干枚，依任意方式依次貼在信封右上角，其面值總和恰為n分，不同的排列方式為不同貼法，求有多少種郵票貼法?這就是郵票排列問題。

郵票排列問題的計數多項式為，若用p枚郵票依此貼上，其值總和為n分，則貼法數等於)展開式中x的係數。因此，郵票貼法總數A_n的計數生成函式是

這裡規定等於中xⁿ的係數，滿足遞歸關係：，這裡規定。

例題解析

先看第一個問題。

【例1】設是一組給定的正整數，n是任意正整數。令A_n表示下列不定方程式(又稱Diophantus方程)

的非負整數解組()的個數，求A_n的發生函式。

與此相應的組合問題自然是：假定有m種事物，今要從中任意選取n個事物，但規定第一種事物取出的個數必須是a₁的倍數，第二種事物必須是a₂的倍數，余類推。因此取出n個事物的組合方法數的發生函式應該是如下形式的連乘積

簡記

自然，F(t)也就是A_n的發生函式，按台勞展開式，還可將A_n表示成

注 此例的整數解組問題又稱為“貨幣兌換問題”，可以構想有m種貨幣，其票面價值各為a₁個單位，a₂個單位，…，a_m個單位，於是A_n即代表把n個單位兌換成各種貨幣的一切組合方法數。

【例2】 (郵票排列問題)寄信需要郵票n分，今用1分、2分、3分、4分四種郵票貼上在一長排上，不同的排列方式算作不同的方法，令B_n表示不同的方法數，試求B_n的發生函式。

注意此題與上題不同，這裡多了個排列方式問題，倘若單純地問：郵局裡只有1、2、3、4分四種郵票，問買足幾分郵票的方法有多少種，這就成了貨幣兌換問題，由上例知其發生函式為。

此題相當於：用1，2，3，4四數為項作和，以求其能加得為正整數n的一切方法數B_n，如果規定用k個項相加表出n，則方法數顯然等於展開式中t_n的係數，因此關於一切方法總數B_n的發生函式便是