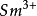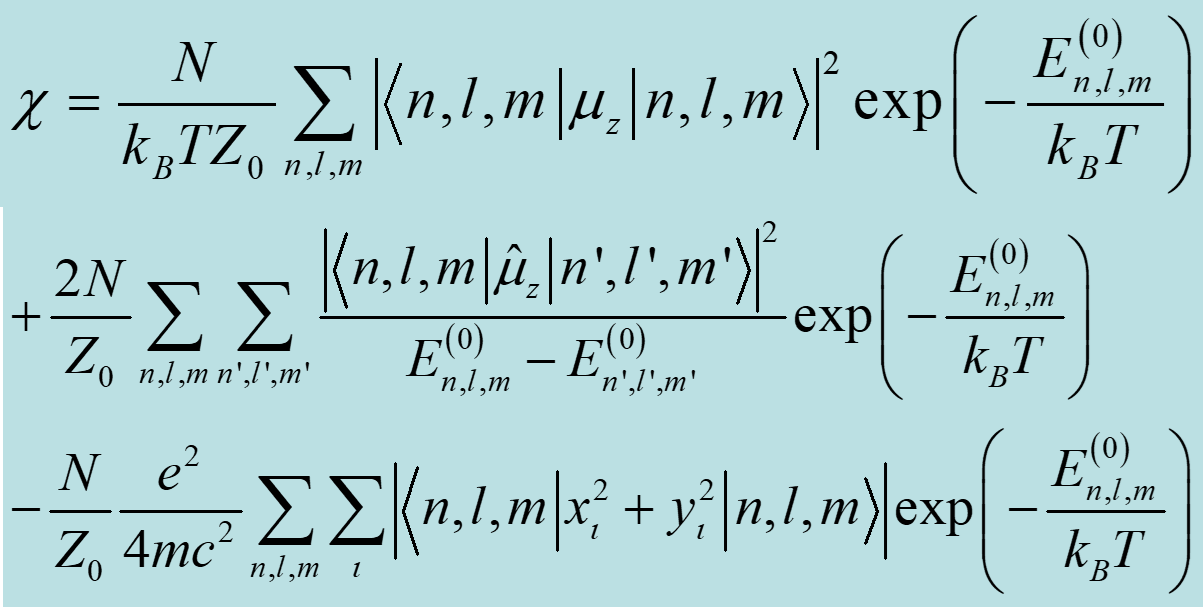本世紀初,Langevin和Debye提出了順磁性的經典理論.在量子力學出現後,VanVleck發展了順磁性的量子理論.在此基礎上,1932年,他導出了原子或離子系統磁化率的普遍公式,這就是廣義的Langevin-Debye公式,簡稱為Langevin-Debve 公式。
基本介紹
- 中文名：朗之萬-德拜公式
- 外文名：langevin-debye formula
推導過程,對范弗萊克順磁性的一些理解,
推導過程
考慮原子磁矩不為零的系統，當磁場不十分強時，同樣用微擾方法求出體系的能量，（只保留到
項）
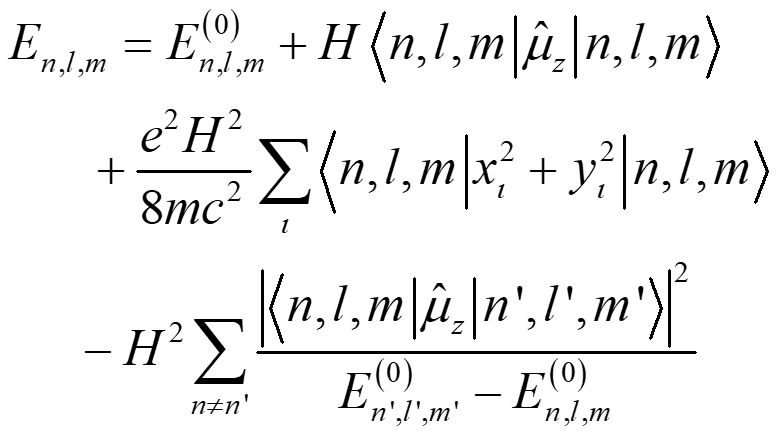
這裡與原子磁矩為零時的區別就在於對原子磁矩不為零的系統原子，微擾中的一階項不再等於零。
玻爾茲曼統計的配分函式為：
系統的磁化率為：
其中 N 為單位體積的原子數,取：
可以計算出順磁磁化率的表達式為：
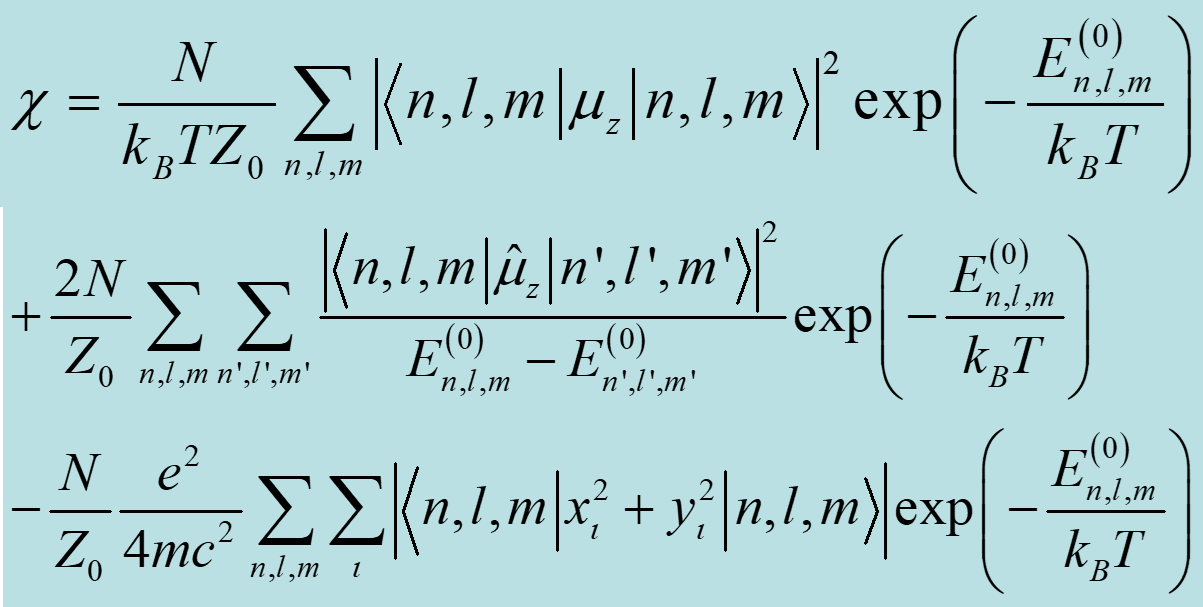
該式稱作朗之萬- 德拜公式，其中第三項就是前面給出的抗磁磁化率項。頭兩項是順磁磁化率，第一項是取向順磁磁化率，和朗之萬經典結論相似，與溫度有關。
第二項是激發態對順磁性的貢獻，與溫度基本無關。一般情況下比第一項小得多，稱之為：范弗萊克（Van Vleck) 順磁性。
對范弗萊克順磁性的一些理解
在近似計算自由原子（離子）的順磁性時，我們忽略了磁場對本徵波函式的作用，然而事實上， B≠ 0 時的本徵波函式不同於B = 0 時的本徵波函式，B≠ 0 時的本徵波函式是B = 0 時未受擾的一些本徵波函式的組合，結果使非干擾狀態的磁矩發生變化，這種作用對磁化率的貢獻首先是范弗萊克用微擾理論計算出來的，也稱為范弗萊克順磁性。
Van Vleck 順磁性來源於磁場對電子云的形變，即二級微擾使激發態混入基態，使電子態發生微小的變化所致，它常是對順磁性和抗磁性的一個修正，且基本不依賴於溫度。
范弗萊克量子理論很好的揭示了過渡族元素和稀土族元素間的差異，並指出稀土元素 Sm+3和Eu+3 的特殊性，揭示了它們的原子磁矩偏離洪德法則的原因。
雖說原則上可以利用范弗萊克量子理論計算任何原子的磁化率，但實際上是很困難的，需要繁瑣而複雜的量子力學計算。
小結： 范弗萊克量子理論正確處理了順磁性和抗磁性的問題，揭示了它們之間的內在聯繫，指出了除去原子磁矩的取向效應外，還存在一個與溫度無關的順磁效應——范弗萊克順磁性。
他既肯定了 Langevin 經典理論正確的一面，又指出了經典理論的不足，成功地解釋了複雜多變的實驗結果。
具體的講，范弗萊克量子理論的結果，按激發能量 Δ 的大小可以區分為如下三種不同的情況：
（1）當 Δ << kBT 時，激發態離基態非常近，原子具有不同能態的機率較大，可以證明：這時的磁化率仍具有居里定律的形式。過渡族元素的順磁性屬於這種情況。
（2）當 Δ>> kBT 時，激發態能量很高，離基態較遠。這時，大部分原子仍處在基態。可以證明：這時激發態的影響將導致一項與溫度無關的順磁化率。
（3）當
時，激發態離基態不遠。這時磁化率與溫度的關係比較複雜，不同於居里定律的形式。稀土離子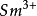
和
就屬於這種情況。用 
的計算結果與實驗相差較大。
