對給定的覆蓋單元集F,設圖G所有邊(點)覆蓋所構成的集族為J,對每一覆蓋S∈J,將一個單項式X(S)定義為Πα∈Swα,進而對圖G賦以一個多項式P(G),定義ΣS∈JX(S),這個P(G)便稱為圖G在F之下的“邊(點)覆蓋多項式”。
基本介紹
- 中文名:邊覆蓋多項式
- 所屬學科:數學(圖論)
- 性質:圖的一種多項式
- 相關概念:點覆蓋,簡單圖,覆蓋單元集等
基本介紹
相關定義












邊覆蓋多項式的定義











舉例分析



























基本定理
















邊覆蓋多項式的消去定理










點覆蓋多項式的消去定理
















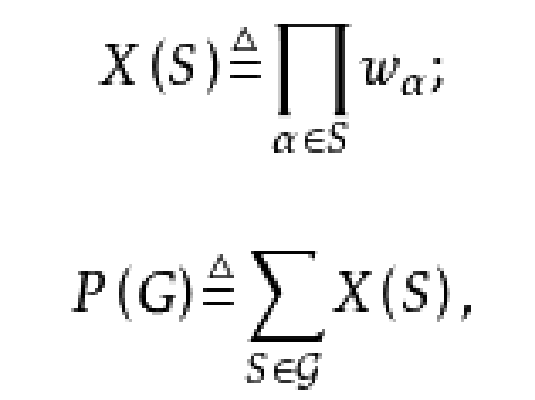
對給定的覆蓋單元集F,設圖G所有邊(點)覆蓋所構成的集族為J,對每一覆蓋S∈J,將一個單項式X(S)定義為Πα∈Swα,進而對圖G賦以一個多項式P(G),定義ΣS∈JX(S),這個P(G)便稱為圖G在F之下的“邊(點)覆蓋多項式”。




























































































對給定的覆蓋單元集F,設圖G所有邊(點)覆蓋所構成的集族為J,對每一覆蓋S∈J,將一個單項式X(S)定義為Πα∈Swα,進而對圖G賦以一個多項式P(G),定義ΣS∈JX(S),這個P(G)便稱為圖G在F之下的“邊(點)覆...
覆蓋函式有兩種,分別是全局覆蓋函式和局部覆蓋函式。當前數值流形法多採用基於全局坐標的多項式覆蓋函式(簡稱全局覆蓋函式)。部覆蓋函式使得在物理覆蓋區域內的單元剛度矩陣與單元的具體位置無關,即與單元距坐標原點的遠近無關,使剛度矩陣的...
雙循環空間的一組基稱為雙圈基,雙循環空間的維數稱為雙圈秩,與某一雙圈基中的每一個圈恰有一條公共邊的邊集,稱為雙樹。子圖多項式與秩多項式 子圖多項式 當G為無向圖,由G的一切連通子圖所構成時,圖G在 之下的點覆蓋多項式...
是由覆蓋變換產生的同源圓 。更普遍如果 是一個三維流形 它有一個亞歷山大多項式 定義為其無窮循環覆蓋空間的階理想。在這種情況下 是等號的,等於扭力子群的順序 。眾所周知,每一個對稱的積分Laurent多項式都是1的單位,是一個結的...
本項目是對最小連通感測器覆蓋等 NP 難度最佳化問題的多項式時間近似算法的設計與分析。所選出的問題理論難度大,套用背景強。因此,研究結果對算法理論與無線感測器網路技術的發展均有重要意義。結題摘要 覆蓋問題是在無線感測網路研究中的...
第一個在最壞情況具有多項式時間複雜度的線性規划算法在1979年由前蘇聯數學家Leonid Khachiyan提出。這個算法建基於非線性規劃中Naum Shor發明的橢球法(ellip-soid method),該法又是Arkadi Nemirovski(2003年馮‧諾伊曼運籌學理論獎得主...
Misra&Gries(1992)和Gabow等人(1985)描述了用Δ+ 1顏色著色任何圖的多項式時間算法,滿足Vizing定理給出的界限;見Misra&Gries邊緣著色算法。對於多重圖像,Karloff&Shmoys(1987)提出了以下算法,它們歸功於Eli Upfal。通過將邊緣連線...
本項目的代表性成果如下:(1)對於圖的匹配覆蓋問題(用最少的匹配覆蓋圖的頂點),給出了多項式時間算法:一般圖的時間界是O(n3),樹的時間界是O(n);同時給出匹配覆蓋數的界和樹情形匹配覆蓋數的精確刻畫。該論文2014年發表在...
近似算法比較經典的問題包括:最小頂點覆蓋、旅行售貨員問題、集合覆蓋等。迄今為止,所有的NP完全問題都還沒有多項式時間算法。對於這類問題,通常可採取以下幾種解題策略。(1)只對問題的特殊實例求解 (2)用動態規劃法或分支限界法求解...
由於一個置換可以做環狀分解,可以看出一個置換與一個可能的圈覆蓋是一一對應的。特別的,G的鄰接矩陣的積和式即是G中圈覆蓋的數目。計算複雜性 積和式的計算是#P完全的。相對的,行列式可以用高斯消元法等算法在多項式時間內解決。
P和NP對於一個問題,如果存在一個圖靈機,對這個問題的任何實例,都能給出回答,那么這個問題就稱作可解的;如果存在一個圖靈機,又存在一階多項式P,在給定問題的實例後(設n是給定實例在0、1編碼下的長度),這個圖靈機能在P(n)...
