在圖論中,圖形的邊緣著色是將“顏色”分配給圖形的邊緣,使得沒有兩個相鄰邊緣具有相同的顏色。 例如,左圖顯示紅色,藍色和綠色的圖形的邊緣著色。 邊緣著色是幾種不同類型的圖形著色之一。 邊緣著色問題考慮的是是否可以使用最多k個不同顏色,給定的k值或最少可能的顏色對給定圖形的邊緣進行著色。 給定圖形邊緣所需的最少顏色數量稱為圖形的邊色數。
基本介紹
- 中文名:邊色數
- 外文名:Edge coloring
- 學科分類:數學
- 涵義:給定圖形邊緣所需的最少顏色數量
- 領域:光纖網路的調度、頻率分配
- 常見問題:循環賽
簡介,例子,定義,匹配關係,算法,最佳著色特殊類圖,使用超過最佳顏色數量的算法,精確算法,套用,
簡介
在圖論中,圖形的邊緣著色是將“顏色”分配給圖形的邊緣,使得沒有兩個相鄰邊緣具有相同的顏色。 例如,右圖顯示紅色,藍色和綠色的圖形的邊緣著色。 邊緣著色是幾種不同類型的圖形著色之一。 邊緣著色問題考慮的是是否可以使用最多k個不同顏色,給定的k值或最少可能的顏色對給定圖形的邊緣進行著色。 給定圖形邊緣所需的最少顏色數量稱為圖形的邊色數。 例如,圖中的圖形的邊緣可以用三種顏色著色,但是不能用兩種顏色著色,因此所示的圖具有三色指數。 幾何構造的7邊緣著色的完整圖
幾何構造的7邊緣著色的完整圖
 幾何構造的7邊緣著色的完整圖
幾何構造的7邊緣著色的完整圖通過維格定理,邊緣顏色所需的顏色數量是一個簡單的圖形,或者是其最大度Δ或Δ+ 1。對於一些圖形,如二分圖和高度平面圖,顏色數量始終為Δ,而對於多重圖形,顏色數量可能大至3Δ/ 2。 有多項式時間算法構建二分圖的最佳著色,以及最多使用Δ+ 1顏色的非二分圖簡單圖的著色;然而,找到最佳邊緣著色的一般問題是NP-hard,並且其最快的已知算法具有指數時間。 已經研究了邊緣著色問題的許多變化,其中顏色對邊緣的分配必須滿足除非鄰接之外的其他條件。 邊緣著色在光纖網路的調度問題和頻率分配中具有套用。
例子
如果循環邊緣的長度是偶數,循環圖可能會有兩種顏色的邊緣:簡單地在周期周圍交替兩種顏色。 然而,如果長度是奇數,則需要三種顏色。
當n為偶數時,具有n個頂點的完整圖形Kn具有n-1個顏色的邊緣可著色;這是鮑勞尼奧伊定理的一個特例。 Soifer(2008)在這種情況下提供著色的以下幾何構造:將n個點放置在常規(n-1)面多邊形的頂點和中心。 對於每個顏色類,包括從中心到其中一個多邊形頂點的一個邊,以及連線多邊形頂點對的所有垂直邊。 然而,當n是奇數時,需要n個顏色:每個顏色只能用於(n-1)/ 2個邊,總和的1 / n分數。
幾位學者研究了奇數圖的邊緣著色,n個正則圖,其中頂點代表從2n-1個玩家池中選出的n-1個玩家的佇列,其中邊緣表示這些隊伍的可能配對(一個 玩家離開為“奇怪的人”來裁判比賽)。 n = 3的情況給出了眾所周知的Petersen圖。 由於Biggs(1972)解釋了這個問題(對於n = 6),玩家希望找到這些配對的時間表,使得每個隊伍在一周的不同日子裡玩六場比賽,所有隊伍的星期日休息;也就是說,在數學上形式化問題,他們希望找到6個常規奇數圖O6的6邊緣著色。 當n為3,4或8時,On的邊緣著色需要n + 1種顏色,但是當它為5,6或7時,只需要n種顏色。
定義
與其頂點對應一樣,當沒有任何限定的情況下,圖形的邊緣著色總是被認為是邊緣的正確著色,意味著沒有兩個相鄰的邊被分配相同的顏色。這裡,當共享共同的頂點時,兩個邊被認為是相鄰的。
使用k種不同顏色的正確邊緣著色被稱為(正確的)k邊緣著色。可以分配(正確的)k邊緣著色的圖形被稱為k邊緣可著色。曲線G的(正確)邊緣著色所需的最小顏色數量是色度指數或邊緣色數χ'(G)。彩色指數也有時用χ1(G)表示;在這個符號中,下標表示邊緣是一維對象。如果其色彩指數正好為k,則圖形為k邊緣色。顏色指數不應與色數χ(G)或χ0(G)混淆,即G中適當頂點著色所需的最少顏色數。
除非另有說明,否則所有圖都被認為是簡單的,與其中兩個或多個邊緣可以連線同一對端點並且其中可能存在自迴路的多個圖形相反。對於邊緣著色中的許多問題,簡單圖表的行為與多重圖形不同,需要額外注意將簡單圖形邊緣著色的定理擴展到多圖案。
匹配關係
下圖中的匹配是一組邊,其中沒有兩個相鄰;完美匹配是一個匹配,包括邊緣觸摸圖的所有頂點,並且最大匹配是包括儘可能多邊緣的匹配。在邊緣著色中,具有任何一種顏色的邊緣集必須彼此不相鄰,因此它們形成匹配。也就是說,正確的邊緣著色與圖形的分割與不相交的匹配是相同的。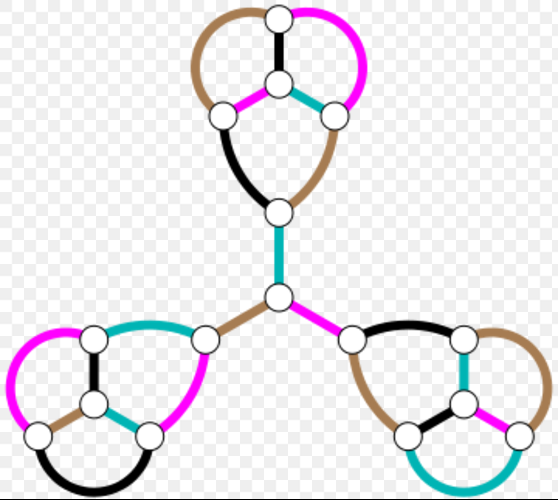 3規則平面圖具有16個頂點和24個邊
3規則平面圖具有16個頂點和24個邊
 3規則平面圖具有16個頂點和24個邊
3規則平面圖具有16個頂點和24個邊如果給定圖形中最大匹配的大小很小,則需要許多匹配來覆蓋圖形的所有邊。更正式地表達,這個推理意味著如果圖形總共有m個邊,並且如果最多β個邊緣可能屬於最大匹配,則圖形的每個邊緣著色必須至少使用m /β個不同的顏色。例如,圖中所示的16頂點平面圖具有m = 24邊。在這個圖中,沒有完美匹配;因為如果中心頂點匹配,剩餘的不匹配頂點可以被分組成具有四個,五個和五個頂點的三個不同的連線分量,並且具有奇數個頂點的分量不能完全匹配。然而,圖形具有七個邊緣的最大匹配,所以β= 7。因此,圖形邊緣顏色所需的顏色數量至少為24/7,由於顏色數必須是整數,因此至少是四。
對於沒有完美匹配的度數k的常規圖,該下限可以用於顯示至少需要k + 1種顏色。特別地,對於具有奇數個頂點(例如奇數完整圖形)的常規圖形,這是正確的。對於這樣的圖表,通過握手引文,k本身就是平等的。然而,不等式χ'≥m/β並沒有完全解釋每個常規圖的色度指數,因為有規則的圖確實有完美的匹配,但不是k邊緣可著色。例如,Petersen圖是規則的,m = 15,β= 5邊緣完美匹配,但它沒有3邊緣著色。
算法
因為測試圖形是否為1類的問題是NP完成,所以沒有已知的多項式時間算法用於對每個具有最佳顏色數的圖形進行邊緣著色。 然而,已經開發了許多放鬆以下一個或多個標準的算法:它們僅在圖的子集上工作,或者它們並不總是使用最佳數量的顏色,或者它們並不總是在多項式時間內運行。
最佳著色特殊類圖
在具有最大程度Δ的二分圖或多幅圖的情況下,最佳顏色數量恰好為Δ。 Cole,Ost&Schirra(2001)表明,這些圖的最佳邊緣著色可以在近線性時間界O(m logΔ)中找到,其中m是圖中的邊數;Cole&Hopcroft(1982)和Alon(2003)描述了更簡單但更慢的算法。 Alon(2003)的算法開始於通過合併屬於同一側的頂點對,然後添加少量附加頂點和邊緣。那么,如果程度是奇數,Alon會在近似線性的時間內找到一個完美的匹配,為它分配一個顏色,並將其從圖中刪除,從而導致程度變得均勻。最後,Alon套用Gabow(1976)的觀察,在圖的歐拉之旅中選擇交替的邊緣子集將其劃分為兩個常規子圖,將邊緣著色問題分解成兩個較小的子問題,並且他的算法解決了兩個子問題遞歸。他的算法的總時間是O(m log m)。
對於最大度Δ≥7的平面圖,最佳顏色數量再次精確為Δ。通過Δ≥9的更強的假設,可以線上性時間內找到最優邊緣著色。
使用超過最佳顏色數量的算法
Misra&Gries(1992)和Gabow等人(1985)描述了用Δ+ 1顏色著色任何圖的多項式時間算法,滿足Vizing定理給出的界限;見Misra&Gries邊緣著色算法。
對於多重圖像,Karloff&Shmoys(1987)提出了以下算法,它們歸功於Eli Upfal。通過將邊緣連線的新頂點添加到每個奇數頂點,找到歐拉之旅,並選擇旅遊方向,使輸入多重G歐拉。形成二分圖H,其中G的每個頂點有兩個副本,一個在兩分區的每一側,一個從兩分區左側的頂點u的邊緣到兩分區右側的頂點v每當面嚮導游從u到v的邊緣時,套用二分圖邊緣著色算法。H中的每個顏色等級對應於G中的一組邊,形成最大二度的子圖;也就是說,路徑和循環的不相交的結合,所以對於H中的每個顏色類,可以在G中形成三個顏色等級。算法的時間由時間到邊緣顏色的二分圖O(m log Δ),使用Cole,Ost&Schirra(2001)的算法。該算法使用的顏色數量至多為3△/2,接近但不完全相同於3△/2。它也可以以直接的方式形成並行算法。在同一篇文章中,Karloff和Shmoys還提出了一種線性時間算法,用於以類似原理操作的四種顏色(符合香農和Vizing的邊界)著色最大三度的多重圖像:它們的算法添加了一個新的頂點,使圖表為歐拉,找到歐拉之旅,然後在巡視中選擇交替的邊緣組,將圖形分解成最大二度的兩個子圖。每個子圖的路徑和均勻循環可以用每個子圖的兩種顏色著色。在此步驟之後,每個剩餘的奇數周期包含至少一個邊緣,可以用屬於相反子圖的兩種顏色之一來著色。從奇數周期中刪除該邊緣可以使用兩個顏色為其子圖進行著色。
一個將圖形或多重圖形的邊緣逐一考慮的貪婪著色算法有時會使用多達2Δ-1種顏色,這可能是所需顏色數量的兩倍。然而,其優點是可以在輸入圖預先未知的線上算法設定中使用;在這種情況下,其競爭比例為2,這是最佳的:沒有其他線上算法可以實現更好的性能,然而,如果邊緣以隨機順序到達,並且輸入圖具有至少為對數的程度,則可以實現較小的競爭比。
幾位作者提出了一些猜想,這意味著任何多重圖形的分數色度指數(可以使用線性規劃在多項式時間內計算的數字)都在一個色度指數之內。如果這些猜想是真實的,則可以從多圖案中的色度索引中計算一個從不會超過一個的數字,匹配通過Vizing的定理了解簡單圖。雖然未經證實,但是當色度指數至少為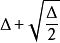 時,這些猜想是已知的,因為可能發生在具有足夠大的多重性的多幅圖。
時,這些猜想是已知的,因為可能發生在具有足夠大的多重性的多幅圖。
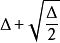
精確算法
測試圖形是否可以用一種或兩種顏色進行邊緣著色是直接的,因此邊緣著色的第一個非平凡的情況是測試圖形是否具有3邊緣著色。如Kowalik(2009)所示,可以在使用多項式空間的同時,測試圖形在時間O(1.344n)中是否具有3邊緣著色。雖然這個時間限制是指數的,但是它比對邊緣顏色的所有可能分配的強力搜尋要快得多。每個具有n個頂點的雙連通3正則圖具有O(2n / 2)3邊緣著色;所有這些都可以在時間O(2n / 2)中列出(比找到單一著色的時間稍慢),正如Greg Kuperberg所觀察到的那樣,n / 2邊多邊形上的稜鏡的圖形有很多的著色,表明這個邊界很緊。
通過對輸入圖的線圖套用精確的頂點著色算法,可以在時間為2mmO(1)和指數空間的情況下,無論所需的顏色數量如何,都可以對m個邊緣進行最佳邊緣顏色邊緣顏色,或者在時間O(2.2461m)和唯一多項式空間(Björklund,Husfeldt&Koivisto 2009)。
因為即使對於三種顏色,邊緣著色也是NP完成的,當參數化顏色數量時,不太可能會固定參數。但是,對於其他參數來說,這是很容易的。特別地,Zhou,Nakano&Nishizeki(1996)顯示,對於樹寬w的圖,可以在時間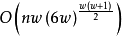 中計算最優邊緣著色,一個依賴於w,但僅在圖中頂點數n上呈線性關係。
中計算最優邊緣著色,一個依賴於w,但僅在圖中頂點數n上呈線性關係。
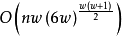
Nemhauser&Park(1991)將邊緣著色問題制定為整數程式,並使用整數規劃求解器描述其使用邊緣顏色圖的經驗。然而,他們沒有對其算法進行任何複雜性分析。
套用
完整圖形的邊緣著色可用於將循環賽進行儘可能少的輪次,以便每對競爭對手在一輪中相互對峙;在這個套用中,圖形的頂點對應於比賽中的競爭對手,邊緣對應於遊戲,邊緣顏色對應於玩遊戲的回合。類似的著色技術也可用於安排不是全部播放的其他運動配對;例如,在國家橄欖球聯盟中,根據前一年的隊伍記錄,確定了在一年中相互發揮的成對隊伍,然後將邊緣著色算法套用於由一組配對,以便將遊戲分配給他們玩的周末。對於這個套用,維格定理意味著,無論選擇什麼組合(只要沒有球隊在同一個賽季打兩場比賽),總是有可能找到一個比周末多出一個周末的時間表每隊比賽。
開放車間調度是調度生產過程的問題,其中存在要製造的一組對象,每個對象具有要在其上執行的一組任務(以任何順序),並且每個任務必須以特定的機器,防止需要同一台機器同時執行的任何其他任務。如果所有任務具有相同的長度,那么這個問題可以被形式化為一個二分法多邊形的邊緣著色之一,其中兩分區一側的頂點表示要製造的對象,雙分區的另一側的頂點表示製造機器,邊緣表示必須執行的任務,顏色表示可以執行每個任務的時間步驟。由於可以在多項式時間內進行二次邊緣著色,所以對於開放車間調度的限制情況也是如此。
Gandham,Dawande&Prakash(2005)研究了感測器網路上的時分多址網路通信協定的鏈路調度問題,作為邊緣著色的一個變體。在這個問題中,必須為無線通信網路的邊緣選擇時隙,以便網路的每個節點能夠與每個相鄰節點通信而不受干擾。使用強烈的邊緣著色(並為每個邊緣顏色使用兩個時隙,每個方向一個)將解決問題,但可能需要更多的時間段。相反,他們尋求通過使網路的每個無向邊緣加倍形成的有向圖的著色,其特徵在於每個有向邊緣uv具有與從v離開的邊緣和從v的鄰居出發的邊緣不同的顏色,他們提出了基於用於(Δ+ 1)-edge著色的分散式算法與重新調整可能相互干擾的邊緣的後處理階段的該問題的啟發式。
在光纖通信中,路徑著色問題是將顏色(頻率的光)分配給希望彼此通信的節點對的問題,以及通過每對的光纖通信網路的路徑,受到限制沒有兩條共享纖維段的路徑使用相同的頻率。通過相同通信交換機但不通過任何光纖段的路徑被允許使用相同的頻率。當通信網路被布置為星形網路時,將單箇中央交換機通過單獨的光纖連線到每個節點,路徑著色問題可以被精確地模擬成邊緣著色圖形或多重圖像的問題,其中通信節點形成圖形頂點,希望從圖形邊緣通信的節點對,並且可以用於每一對的頻率形成邊緣著色問題的顏色。對於具有更一般樹形拓撲的通信網路,可以將網路中每個交換機定義的星形網路的本地路徑著色解決方案一起進行修補,以形成單一的全局解決方案。

