把兩個或兩個以上的構件通過運動副的聯接而構成的相對可動的系統稱為運動鏈(kinematics chain)。
基本介紹
- 中文名:運動鏈
- 外文名:kinematics chain
- 組成:兩個或兩個以上的構件通過運動副
- 分類:閉鏈,開鏈
- 包括:閉式運動鏈 開式運動鏈
類型

表示方法
結構簡圖
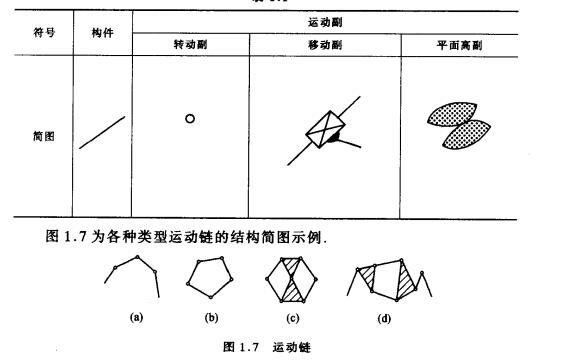 結構簡圖
結構簡圖拓撲圖
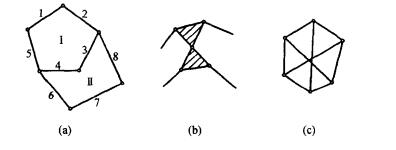 迴路及樹
迴路及樹自由度類型及判定
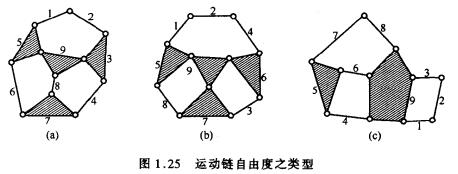 自由度類型
自由度類型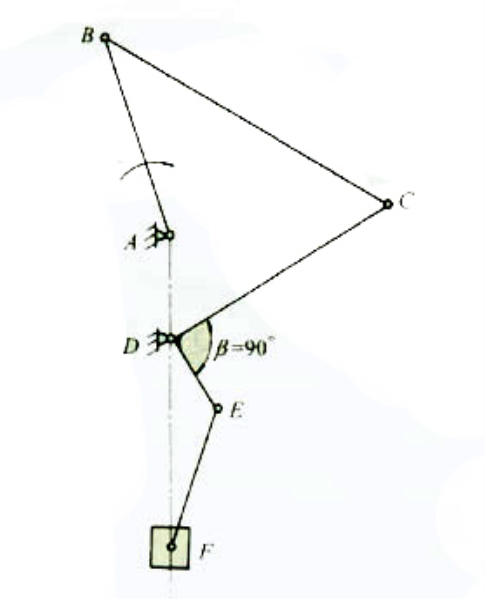
把兩個或兩個以上的構件通過運動副的聯接而構成的相對可動的系統稱為運動鏈(kinematics chain)。

 結構簡圖
結構簡圖 迴路及樹
迴路及樹 自由度類型
自由度類型把兩個或兩個以上的構件通過運動副的聯接而構成的相對可動的系統稱為運動鏈(kinematics chain)。...
何物體的機械運動都是在一定的空間和時間中進行的。人體和器械的運動也不例外。物體的運動在空間和時間等方面所表現出的差異特徵稱運動學特徵。如物體運動的軌跡、...
若組成運動結構的所有構件都在同一平面或相互平行的平面內運動,則稱該結構為平面運動結構。 平面運動結構是具有確定運動的構件系統,其組成要素有構件和運動副。所有...
開鏈運動(Open Kinetic Chain,OKC):是指肢體近端固定而遠端關節活動的運動。進行肌肉鍛鍊的一種方式。...
中文名稱 四桿運動鏈 英文名稱 four bar linkage 定義 具有四個構件的低副運動鏈。 套用學科 機械工程(一級學科),機構學(二級學科),連桿機構(三級學科) ...
樹狀運動鏈編輯 鎖定 本詞條缺少信息欄、名片圖,補充相關內容使詞條更完整,還能快速升級,趕緊來編輯吧!中文名稱 樹狀運動鏈 英文名稱 tree like kinematic chain...
連桿機構(Linkage Mechanism)又稱低副機構,是機械的組成部分中的一類,指由若干(兩個以上)有確定相對運動的構件用低副(轉動副或移動副)聯接組成的機構。平面連桿...
如果在一個機構中加上或減掉一個運動鏈而機構的自由度能夠保持不變,則由最少的構件和運動副組成的這種運動鏈就稱為基本桿組。...
並在線上器人,英文名為Parallel Mechanism,簡稱PM,可以定義為動平台和定平台通過至少兩個獨立的運動鏈相連線,機構具有兩個或兩個以上自由度,且以並聯方式驅動的一種...
本書系統地論述了機器人機構自由度分析的理論和方法,主要內容包括:運用實例指出依據構件個數和運動副約束個數簡單代數求和原理的機構自由度計算方法,以及計算結果常與...
3.3.2運動副的自由度3.3.3運動鏈第4章機械系統方案構思和交流的工具4.1機構運動簡圖的定義4.1.1如何表示機構的運動4.1.2機構運動簡圖的作圖規則4.2機構運動簡圖...
第3章多體系統運動學313.1運動鏈的結構313.1.1拓撲建模313.1.2運動學建模323.2運動鏈中的運動副333.2.1空間運動鏈中的運動副34...
8.4.3 附加上第5個四邊形運動鏈 8.4.4 整體6網眼機構 參考文獻 第9章 機構奇異下的自由度 9.1 機構奇異的分類 9.2 3/3-SPUStewart機構主奇異下自由度 9.3 ...
1.2.1 機構與機器人的基本組成元素:構件與運動副1.2.2 運動鏈、機構與機器人1.2.3 自由度、活動度與約束1.2.4 機器人機構的分類...
第一節人體運動鏈系統與擒拿概述………(15)一、骨、骨連結、運動鏈系統與擒拿………(16)二、運動偶、效應性運動和鎖定效應在擒拿中的套用...
吊籃運輸機是在兩根閉路鏈帶上,每隔一定距離懸掛一個吊籃,吊籃上可擱置墊板,欲乾燥的坯體放在板上,由傳動鏈輪帶動鏈帶使整個吊籃運輸機運動。因吊籃與鏈帶鉸接,...
若組成機構的所有構件都在同一平面或相互平行的平面內運動,則稱該機構為平面機構。 機構是具有確定運動的構件系統,其組成要素有構件和運動副。所有構件的運動平面都...
上篇機構的運動設計1機構的組成和結構101.1機構的組成101.2機構運動簡圖141.3運動鏈成為機構的條件191.4機構的組成原理和結構分析26...
6.3運動鏈組合6.3.1圖的概念6.3.2圖的組合6.3.3運動鏈的組合6.4機構再生設計6.4.1飛機起落架的再生設計6.4.2縫紉機送布機構的再生設計...
第三章敘述了機構和機器人操作手運動學,充分運用了它的幾何特徵,將矩陣方法運用到最一般的機構運動鏈中。第四章和第五章敘述了套用廣泛的曲線和曲面模型。第六章...
多面加工橋架可以定義為動平台和定平台通過至少兩個獨立的運動鏈相連線,機構具有兩個或兩個以上自由度,且以並聯方式驅動的一種閉環機構。...
