運動公理(axiom of motion)是契約公理的另一種表現形式，平面上的運動公理組包括下面六條公理：1.運動把點變為點，把直線變為直線，並且保持結合關係和順序關係。2.存在這樣的運動，把每一個點，每一條直線變為本身，稱為恆等運動。3.一個運動之後繼以另一運動稱為這兩個運動的乘積，任意兩個運動的乘積仍是運動，對於每個運動必存在另一個運動，使這兩個運動的積是恆等運動。4.若運動把某條射線和它的端點變為本身，則射線上的每一點都變為本身。5.若A，B，C是某一圖形中不在同一直線上的三點，則存在惟一一個運動，使圖形按下面的方式變為另一圖形：1) 點A變為已知點A′；2) 點B變為以A′為端點的已知射線h′上的某一點B′，即射線AB變為射線A′B′；3) 點C變為射線h′已知一側的某一點C′。6.存在運動把線段AB變為BA;也存在運動把∠AOB變為∠BOA。在構造歐氏幾何的公理系統時，可採用運動公理組代替與其等價的契約公理組。
基本介紹
- 中文名：運動公理
- 外文名：axiom of motion
- 所屬學科：數學
- 所屬問題：高等幾何(幾何基礎)
- 簡介：契約公理的另一種表現形式
基本介紹,相關定理,
基本介紹
在希爾伯特所提出的歐氏幾何公理組Ⅰ一Ⅴ中，在組Ⅲ里的“契約”作為基本概念，運動作為派生概念。為了把公理法與克萊因的群論原則結合起來，在希爾伯特之後，就有一些幾何專家依照歐幾里得在“原本”里的思想，以“運動”為基本概念，而把運動下的對應圖形定義為契約圖形。關於運動，則用以下10條公理來規定。
公理Ⅲ'1 運動是平面到自身(或空間到自身)的變換，它把點變為點，直線變為直線(平面變為平面)。
公理Ⅲ'2 運動把在直線上的點變為像直線上的點。
公理Ⅲ'3 運動把共線上有序三點變為像直線上同序三個像點。
公理Ⅲ'4存在一個運動把平面上的每個點變成自身(恆等變換)。
公理Ⅲ'5 任意兩個運動的乘積仍是一個運動。
公理Ⅲ'6 對於每個運動必存在一運動使得這兩個運動的乘積為恆等變換(逆運動)。
公理Ⅲ'7若運動把某條射線和它的頂點變為自身，那么射線上各點都變為自身。
公理Ⅲ'8 設在一個平面上有兩個點P與Q，和以它們為頂點的兩射線PA和QB，以及由這兩條為射線所在直線為邊緣的半平面α和β，那么存在唯一運動，把點P變為點Q，射線PA變為射線QB，半平面α變為半平面β。
公理Ⅲ'9 存在運動把線段AB變為線段BA。
公理Ⅲ'10存在運動把角∠(h,k)變為角∠(k,h)。
上述10條公理合成一個公理組Ⅲ'，叫做運動定理。其中公理Ⅲ'9和Ⅲ'10又叫做反射公理。
相關定理
由公理Ⅲ'1-3可推出（以下定理的證明請參考相關文獻）：
定理1 每個運動都把線段變為線段，射線變為射線，半平面變為半平面。
在組Ⅰ、Ⅱ的基礎上，組Ⅲ'與Ⅲ是等價的。下面舉例說明。
定理2 設A和B是直線a上的兩個點，又A'是同一直線或另一-條直線a'上的點，則在直線a'上點A'的任意指定的一側存在唯一一點 B'，使得線段AB= A'B'。
證明： 設點A'是直線a'上一點，並指定某一側為射線A'B' ，以直線a,a'為邊緣的半平面分別為α和α'，由公理Ⅲ'8可知，存在一個運動f,使得點A變為點A' ，射線AB變為射線A'B',點B變為射線A'B'上的一點B'，即線段AB變為線段A'B'，就是說AB≡A'B'。現證點B'是唯一的。以直線a、a'為邊緣的另一對半平面分別記β和β'，也存在一個運動f'，把點A變為點A' ，射線AB變為射線A'B'，β變為β'，而點B變為點B"。由公理Ⅲ'6知，存在f的逆運動f-1，它把射線A'B'變為AB；又由公理Ⅲ'8知，f'f-1也是一個運動，它把射線A'B'變為射線A'B'，因此根據公理Ⅲ'7，A'B' 上所有點均不變，從而 f'f-1(B')) = B'，但f'f-1(B') = B"，故B' = B"。
定理3圖形
的契約關係滿足：
1.反射性:
。
2.對稱性:若
，則
。
3. 傳遞性：若
，則
。
推論 若線段A'B'= AB，A"B"= AB，則A'B' = A"B”。
定理4 設AB與BC是直線a上而無公共內點的線段，A'B'與B'C'是直線a'(或a=a')上兩條無公共內點的線段，若AB= A'B'，BC= B'C'，則AC= A'C'。
定理5 如圖1所示，設平面α上給定一個角∠(h,k)，在同一個或號一個平面α'上給定直銭a'，而且在平面α'上指定了直線a'的一側，設h'是直線a'上從一點O'出發的射線，那么在平面α'上存在著唯一的一條射銭k'，使得∠(h,k)契約於∠(h',k')；而且∠(h',k')的所有內點都在直線a'所指定的那一側，並且毎個角都與它自身契約，即∠(h,k)= ∠(h',k')；∠(h,k)= ∠(h,k)。
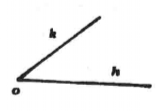圖1（a）
圖1（b）定理6 如果兩個三角形△ABC與△A'B'C'之間滿足：AB≡A'B'，AC≡A'C'，∠BAC≡∠B' A'C'，則∠ABC≡∠A'B'C'，∠ACB≡∠A'C'B'，BC≡B'C'。
