連分式近似

連分式近似(continued fraction approximation)是大規模系統的一種頻域降階法，是函式的一種估值方法，收斂速度比指數序列展開要快，在實際中套用較好。傳遞函式G(s)的連分式展開式有三種基本形式，連分式近似是在G(s)的連分式展開式中捨去某次係數後所獲得的低階模型。

基本介紹

• 中文名：連分式近似
• 外文名：continued fraction approximation
• 屬性：大規模系統的一種頻域降階法
• 所屬學科：數理科學
• 相關概念：連分式，傳遞函式等

基本思想

連分式法是一種有理函式逼近法，其基本出發點是：將原型展開成連分式，然後截取前面幾個起主要作用的偏係數構成簡化模型，連分式法計算簡便，擬合精度較高，是一種很有效的傳遞函式簡化法。

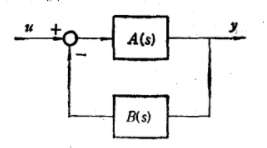圖1 具有負反饋的系統

從物理意義上說，連分式法相當於對複雜的反饋系統取消其中若干個作用較小的內環，然後獲得一個低階的簡化模型，今有一系統如圖1所示。顯然，系統的閉環傳遞函式為

由上式可知，當正向通道 的增益加大時，反饋通道 對 的影響也將加大，若 ，則

式(2)實際上是式(1)的簡化模型。連分式法簡化的機理同上述思路是一樣的。

基本步驟

用連分式法進行模型簡化步驟是： ·

(1) 展開

即將用有理函式表示的傳遞函式 用一定算法展開成某種形式的連分式。

(2) 截斷

即根據簡化模型的階次要求，取連分式的前面若干項偏係數，而將後面各項偏係數截斷，從而得到一個低階的連分式。

(3)反演

即將截斷的低階連分式重新表示為有理函式形式，這樣就得到了簡化模型。下面我們先介紹一下各種形式的連分式。

各種連分式及其物理意義

連分式有很多種形式，常見的有第一Cauer形，第二Cauer形，修正連分式等，下面分別加以介紹。

第一Cauer形

設有一系統，如圖2所示，它的閉環傳遞函式為

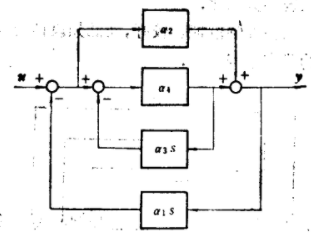圖2具有多個內反饋的系統

(* 為了節省篇幅，後面各連分式均用此簡略寫法。)

若只考慮高頻特性，即 時的特性，則有

即比例環節與慣性環節並聯，在過渡過程起始段(亦即高頻段)比例環節起主要作用，故 可以近似表示為

上面就是第一Cauer形連分式的降階機理。一般地，我們可以將系統的傳遞函式表示為如下形式：

式(6)即為n階的第一Cauer形連分式，與之對應的系統結構圖見圖3，進行模型簡化時，只要取前 項，經過反演，即可得到k階簡化模型。從物理意義上看，也就是通過忽略圖3中系統的內環而使系統得到簡化。

這種簡化方法在高頻段擬合較好，而低頻段擬合較差，反映在時間回響上則為穩態誤差較大。

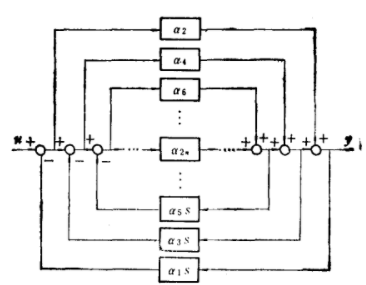圖4第一Cauer形結構圖

第二Cauer形

設有一系統，它的結構圖如圖5所示，它的閉環傳遞函式為

若只考慮低頻段，即 ，可得如下簡化模型：

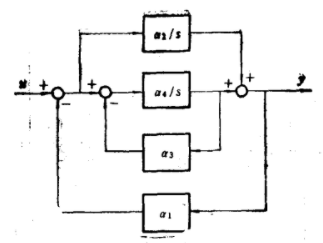圖5 具有多個內反饋的系統

即，積分環節 與慣性環節 並聯，在低頻段積分環節的作用要比慣性環節的作用強，故可將慣性環節忽略。

一般地，我們可以通過展開算法將系統的傳遞函式表示如下

式(9)即為n階的第二Cauer形連分式，與之對應的系統結構圖如圖6所示。

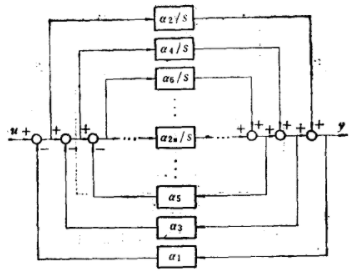圖6 第二Cauer形的結構圖

進行模型簡化時，只要取式(9)的前2k項，經過反演，即可得到k階的簡化模型，從物理意義上看，也就是通過忽略圖6中系統的若干內環而使系統得到簡化。由上面的分析可知，這種簡化方法在低頻段擬合較好，而高頻段擬合較差，反映在時間回響上，瞬態誤差較大。

可以證明，第二Cauer形簡化法與Pade法所得的簡化模型是相同的。

修正連分式

上面所講的兩種Cauer形連分式降階法，一種在高頻擬合較好，另一種在低頻擬合較好，為了兼顧高頻和低頻，有人提出了一種修正連分式法，這就是交替利用兩種Cauer形展開，形如：

進行模型簡化時，取前2k項，經反演即可得k階簡化模型。

帶偏連分式

除了上面介紹的三種連分式外，還有一種靈活性較強的連分式，形式如下

式(11)稱為帶偏連分式，它的前半部分和第二Cauer形一樣，而它的後半部分與第一Cauer形一樣，取不同的r，可以實現有偏重的擬合，當r較大時低頻擬合精度較好，當r較小時高頻擬合精度較好。r取某些特定的值時，帶偏連分式可以轉化為上面幾種連分式，比如r=0，式(11)成為第一Cauer形；r=n，式(11)成為第二Cauer形；r=n/2時，則可以證明式(11)與修正連分式等同。

連分式的展開與反演

要用連分式來進行模型簡化。就必須解決連分式的展開與反演問題，可用長除法等，介紹一種易於用計算機實現的算法．限於篇幅，這裡不討論修正連分式的展開和反演

第一Cauer形

這就是第一Cauer形，並且

第二Cauer形

這就是第二Cauer形，並且