通用編碼是對於統計特性未知的信源所進行的有效編碼。一類以估計信源的機率統計特性為基礎;另一類以序列複雜度理論為基礎。
| 中文名稱 | 通用編碼 |
| 英文名稱 | universal coding |
| 定 義 | 對於統計特性未知的信源進行的有效編碼。一類以估計信源的機率統計特性為基礎;另一類以序列複雜度理論為基礎。 |
| 套用學科 | 通信科技(一級學科),通信原理與基本技術(二級學科) |
基本介紹
- 中文名:通用編碼
- 外文名:universal coding
- 套用學科:通信科技,通信原理與基本技術
起源
分類
信源編碼
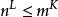
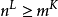
 圖1
圖1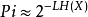
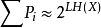
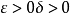
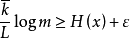
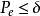
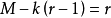
通用編碼是對於統計特性未知的信源所進行的有效編碼。一類以估計信源的機率統計特性為基礎;另一類以序列複雜度理論為基礎。
| 中文名稱 | 通用編碼 |
| 英文名稱 | universal coding |
| 定 義 | 對於統計特性未知的信源進行的有效編碼。一類以估計信源的機率統計特性為基礎;另一類以序列複雜度理論為基礎。 |
| 套用學科 | 通信科技(一級學科),通信原理與基本技術(二級學科) |
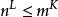
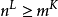
 圖1
圖1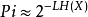
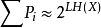
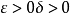
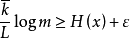
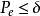
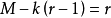
《ISO/IEC 13813:運動圖像及其伴音通用編碼國際標準——MPEG-2》是1997年6月由清華大學出版社出版的圖書,作者是鐘玉琢。內容介紹 運動圖像及其伴音通用壓縮編碼標準是多媒體計算機、多媒體資料庫、多媒體通信、常規電視數位化、高清晰度...
《新一代通用視頻編碼H.266/VVC:原理、標準與實現》是2022年電子工業出版社出版的圖書,作者是萬帥 等。 內容簡介 本書系統全面地介紹了新一代的通用視頻編碼標準H.266/VVC,講解了相關編碼原理和實現方法,並對相應標準語法語義進行...
避免了地址不清、書寫錯誤等問題,方便寄遞企業和廣大用戶。通用寄遞地址編碼的套用場景十分廣泛,如套用於無人機、無人車,實現自動導航和智慧型無接觸服務;連通不同企業的數據信息,實現共同分揀、共同投遞等。
GB13000.1-1993(信息技術 通用多八位編碼字元集(UCS)第一部分:體系結構與基本多文種平面(idt ISO/IEC 10646.1-1993))GB18030-2000(信息交換用漢字編碼字元集 基本集的擴充)不同相互關係 GB 18030完全兼容GBK、GB2312,並且...
4、按照ISIN編碼規則,其最末一位為校驗位。因我國證券交易計算機化程度相當高,為避免編碼資源浪費,對於ISIN編碼的國內基本編碼部分,擬不包含校驗位。5、ISIN編碼是全球通用的、用於識別各個國家或地區證券的唯一代碼,主要用於證券的跨境...
最常見的是信源統計特性已知的離散、平穩、無失真信源編碼。主要方法有:①統計編碼,如仙農碼、費諾碼、赫夫曼碼、算術碼等。②預測編碼。③變換編碼,以及上述方法的組合(混合編碼)。對於信源統計特性未知的信源編碼稱為通用編碼。衡量...
《國家物品編碼通用導則》是2019年7月1日實施的一項中國國家標準。編制進程 2018年12月28日,《國家物品編碼通用導則》發布。2019年7月1日,《國家物品編碼通用導則》實施。起草工作 主要起草單位:中國物品編碼中心、中國人民解放軍國防...
又稱Universal Multiple-Octet Coded Character Set,大陸譯為通用多八位編碼字元集,台灣譯為廣用多八位元編碼字元集。基本概況 通用字元集是所有包括了其他字元集。它保證了與其他字元集的雙向相容,即,如果你將任何文本字元串翻譯...
對限定失真的信源編碼則是以信息率失真R(D)函式為基礎,最典型的是矢量量化編碼。對統計特性未知的信源編碼稱為通用編碼。套用 以簡單的數據壓縮為例即可說明信源編碼的套用。若有一離散、無失真、無記憶信源,它含有五種符號U₀...
通用物品編碼系統 通用物品編碼系統是指跨行業、跨部門、開放流通領域套用的物品編碼系統,是開放流通領域物品的唯一身份標識系統。它包括商品條碼編碼系統和採用射頻識別技術的商品電子編碼系統等。例如:商品條碼編碼系統、商品電子編碼系統、...
2.2 信源編碼的基本概念 2.3 惟一可解碼 2.4 信源變長編碼 2.5 統計匹配碼 習題 第3章 無失真信源編碼方法 3.1 霍夫曼碼和其他編碼方法 3.2 算術編碼 3.3 遊程編碼 3.4 通用編碼 習題 第4章 數學理論基礎 4.1 索數...
國際通用編碼即 zip code,國際通用的郵政編碼方式。美國郵政編碼 (英語:ZIP Code)是美國郵政使用的一種郵政編碼,一般常以大楷寫作ZIP。ZIP是英語:Zone Improvement Plan (地區改進計畫)的簡稱,它暗示郵件可以以更有效率及快捷地送到...
信息交換用漢字編碼字元集 基本集(又稱為GB0)GB 13000 - 93 信息技術 通用多八位編碼字元集(UCS)第一部分 GB 18030 - 2000 信息技術 信息交換用漢字編碼字元集 基本集的擴充 其他中華人民共和國發布有關漢字標準代碼列表:GB/T...
EAN碼(European Article Number)是國際物品編碼協會制定的一種商品用條碼,通用於全世界。EAN碼符號有標準版(EAN-13)和縮短版(EAN-8)兩種。標準版表示13位數字,又稱為EAN13碼,縮短版表示8位數字,又稱EAN8。兩種條碼的最後一...
以利亞加瑪碼(Elias gamma code)是一種用於正整數之通用編碼。該碼由Peter Elias發明。此編碼常被用於無法事先得知上界之正整數。編碼 對於待編碼正整數 :1.令 ,故 2.輸出N個零比特 3.接著輸出X的二進制表示 另一個等價的...
統一碼是一種在計算機上使用的字元編碼,1990年開始研發,1994年正式公布。隨著計算機工作能力的增強,統一碼也在面世以來的十多年裡得到普及。統一碼是基於通用字元集(Universal Character Set)的標準來發展,同時也以出版物的形式(The ...
GB13000 全稱:國家標準GB13000:2010《信息技術 通用多八位編碼字元集(UCS)第一部分:體系結構與基本多文種平面》,此標準等同採用國際標準ISO/IEC 10646-2003,IDT《信息技術 通用多八位編碼字元集(UCS)第一部分:體系結構與基本多...
SC2260 是CMOS工藝製造的低功耗通用編碼器,與SC2272配對使用。編碼器對地址腳和數據腳的狀態編碼組幀以射頻(RF)方式傳送。SC2260 最多有10位三態地址編碼。軟體特點 ● CMOS工藝製造,低功耗 ● 地址碼最多可達59,049(310)種 ...
ASCII (American Standard Code for Information Interchange):美國信息交換標準代碼是基於拉丁字母的一套電腦編碼系統,主要用於顯示現代英語和其他西歐語言。它是最通用的信息交換標準,並等同於國際標準 ISO/IEC 646。ASCII第一次以規範標準...
