通用函式是遞歸證明中常用的一種函式。又稱為枚舉函式。通用函式定理亦稱枚舉定理。
基本介紹
- 中文名:通用函式
- 外文名:universal function
- 適用範圍:數理科學
通用函式定理

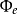
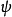
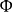
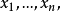
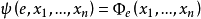
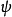

通用函式是遞歸證明中常用的一種函式。又稱為枚舉函式。通用函式定理亦稱枚舉定理。

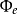
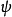
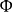
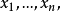
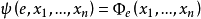
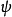
通用函式是遞歸證明中常用的一種函式。又稱為枚舉函式。通用函式定理亦稱枚舉定理。...
通用代碼,也叫通用編程,是一種計算機編程風格,其中算法是根據待指定的類型編寫的,然後在需要時作為參數提供的特定類型進行實例化。 這種方法由ML於1973年開創,允許...
stickline函式,通用格式為stickline(A<B,C,D,N,0),表示含義為在C與D之間畫一條寬度為N。...
函式的定義:給定一個數集A,假設其中的元素為x。現對A中的元素x施加對應法則f,記作f(x),得到另一數集B。假設B中的元素為y。則y與x之間的等量關係可以用y...
標準函式,是具有常用功能的函式。在程式設計中,常將一些常用的功能模組編寫成的函式放在函式庫中供公共選用,一般稱為標準函式。程式是由若干個程式模組組成的,高級...
通用控制系統, 是一種投資小, 通用性好, 組合靈活, 操作簡單, 使用方便, 一機多用, 可適應不同生產對象, 能運行在各種生產環境的高性價比控制系統,可大可小...
在面向對象的多態性中,通用多態表現為參數多態和包含多態兩種多態。...... 在面向對象的多態性中,通用多態表現為參數...但是,函式的參數只能是數據,不能是類型。類...
通用命名規則 UNC (Universal Naming Convention) ,也叫通用命名規範、通用命名約定,指用一種通用語法來描述網路資源(如已分享檔案,目錄或印表機)的位置。例如在...
S-函式是系統函式(System Function)的簡稱,又稱S-function。常用MATLAB編寫。...... 但是,當需要開發一個新的通用的模組作為一個獨立的功能單元時,使用S-函式實現...
約翰.伯努利於1694年首次提出函式(function)概念,並以字母 n 表示變數 z 的一個函式;至 1697年,他又以大寫字母 X 及相應之希臘字母 ξ表示變數 x 的函式。...
函式模板不是一個實在的函式,編譯器不能為其生成可執行代碼。定義函式模板後只是一個對函式功能框架的描述,當它具體執行時,將根據傳遞的實際參數決定其功能。...
隨機函式就是產生數的函式,是EXCEL中很重要的函式,C語言裡也有rand(),srand()等隨機函式。...
光度函式或發光效率函式描述人眼的視覺感知的平均光譜靈敏度。 該函式基於一對不同顏色的光,主觀判斷其中更亮的描述對不同波長光的相對靈敏度。 任何情況下都不...
區域上處處可微分的復函式。17世紀,L.歐拉和J.leR.達朗貝爾在研究水力學時已發現平面不可壓縮流體的無旋場的勢函式Φ(x,y)與流函式Ψ(x,y)有連續的偏導數,...
函式計算器(也稱“科學計算器”)是具有初等函式數值計算功能的一類計算器的總稱,是計算器中最常用的一類。由於生產廠家、型號等的不同而具有不同的計算功能,常用於...
TEXT函式是Excel中一個非常有用的函式。TEXT 函式可通過格式代碼向數字套用格式,進而更改數字的顯示方式。如果要按更可讀的格式顯示數字,或者將數字與文本或符號組合...
回響函式(response function)在網路的輸入端加上激勵信號,則在網路的輸出端便可獲得相應的回響信號。該回響信號稱為回響函式。回響函式可以是電壓回響函式,可以是電流...
小波函式:又稱凌波函式、小波分析(wavelet analysis), 或小波變換、小波轉換(wavelet transform)是指用有限長或快速衰減的、為母小波(mother wavelet)的震盪波形來...
一般的,形如f(x)=ax5+bx4+cx3+dx2+ex+f(a≠0)的函式叫作五次函式。a、b、c、d、e、f對應為其的五、四、三、二、一次項係數與常數。...
函式庫是指可供使用的例行程式和其他電腦程式的集合。可分離函式庫是指函式庫按照某種功能或作用分離成不同的函式模組或組件。可分離函式庫有很多優點:方便對函式...
虛擬函式是C++語言引入的一個很重要的特性,它提供了“動態綁定”機制,正是這一機制使得繼承的語義變得相對明晰。對繼承體系的使用者而言,此繼承體系內部的多樣性是...
信號發生器又稱信號源或振盪器,在生產實踐和科技領域中有著廣泛的套用。各種波形曲線均可以用三角函式方程式來表示。能夠產生多種波形,如三角波、鋸齒波、矩形波(...
CLF(Common Log Format) 是Web伺服器用於記日誌的標準化的格式。此標準化有助於多種日誌分析軟體的通用。
