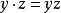逐點乘積

兩個函式的逐點乘積由兩函式在定義域上的每一值的映射相乘得到，仍是一個函式。

基本介紹

• 中文名：逐點乘積
• 學科：數學
• 領域：數學
• 相關術語：卷積定理

介紹

兩個函式的逐點乘積由兩函式在定義域上的每一值的映射相乘得到，仍是一個函式。若f和g都是定義域為X，上域為Y的函式，且Y中的元素可以與其他數相乘（例如Y可以是某個數集），則f與g的逐點乘積是從X到Y的另一個函式，這個函式將x∈X映射到f(x)g(x)。

形式定義

令X和Y為集合，令乘法定義在Y內，也就是說對於Y中的每一y和z，令由 給定的乘積

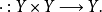
明確定義。令f和g為函式f，g:X→Y，則對於X中的每一x，逐點乘積(f·g):X→Y由下式定義為

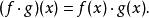
上式在二元運算符·略去時也同樣乘積，其中f·g=fg。

例子

最常見的例子是當上域是乘法明確定義了的環或域時，兩個函式的逐點乘積。

若Y是實數集R，則f，g:X→R的逐點乘積是映射的普通乘法。例如，有函式f(x) = 2x和g(x) =x+ 1，則對於R中的每一實數x，

卷積定理敘述了卷積的傅立葉變換是傅立葉變換的逐點乘積：

代數套用

令X為集合，R為環。因為加法和乘法都在R中有定義，我們可以通過定義函式的逐點加法、乘法和標量乘法，從X到R的函式中構造一個代數結構，這樣的代數稱為k-代數（域上的代數）。

若R標示X到R的函式集，那么就稱若f、g是R的元素，則f+g、fg和rf都是R的元素，其中rf定義為對R中的所有r都有

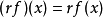
推廣

若f和g都的定義域中包含一組離散變數的所有可能賦值，則它們的逐點乘積是由一個函式，這一函式的定義域是由兩個函式定義域的並集中的所有可能賦值組成。每一賦值的取值由由兩個給定函式值的乘積計算，而二者的賦值子集都在定義域中。

例如，給定布爾變數p和q的函式f₁()與布爾變數q和r的函式f₂()，且二者值域都包含於R，則f₁() 與f₂() 的逐點乘積如下表所示：

p	q	r	f1(p,q)	f2(q,r)	逐點乘積
T	T	T	0.1	0.2	0.1 x 0.2
T	T	F	0.1	0.4	0.1 x 0.4
T	F	T	0.3	0.6	0.3 x 0.6
T	F	F	0.3	0.8	0.3 x 0.8
F	T	T	0.5	0.2	0.5 x 0.2
F	T	F	0.5	0.4	0.5 x 0.4
F	F	T	0.7	0.6	0.7 x 0.6
F	F	F	0.7	0.8	0.7 x 0.8