《透平葉片的載入方法》是東方電氣集團東方汽輪機有限公司於2013年12月20日申請的專利，該專利的公布號為CN103670528A，申請公布日為2014年3月26日，發明人是鄧國梁、孫奇、曹守洪、方宇、吳其林、賀偉、鐘剛雲、古翔。
《透平葉片的載入方法》所述透平葉片的二維葉型的載荷特性通過葉型的幾何參數UGT大小來控制。該發明明確了葉型載荷沿葉高的分布規律的具體情形、控制載荷的程度和控制範圍，在實際的工程設計中，利於大規模套用和推廣，操作性強。
2017年12月11日，《透平葉片的載入方法》獲得第十九屆中國專利優秀獎。
（概述圖為《透平葉片的載入方法》摘要附圖）
基本介紹
- 中文名：透平葉片的載入方法
- 申請人：東方電氣集團東方汽輪機有限公司
- 申請日：2013年12月20日
- 申請號：2013107054050
- 公布號：CN103670528A
- 公布日：2014年3月26日
- 發明人：鄧國梁、孫奇、曹守洪、方宇、吳其林、賀偉、鐘剛雲、古翔
- 地址：四川省德陽市高新技術產業園區金沙江西路666號
- 分類號：F01D5/14(2006.01)I
- 代理機構：成都蓉信三星專利事務所
- 代理人：劉克勤、段雪茵
- 類別：發明專利
專利背景,發明內容,專利目的,技術方案,有益效果,附圖說明,技術領域,權利要求,實施方式,榮譽表彰,
專利背景
透平通流效率很大程度上取決於通流內靜、動葉片的氣動性能。葉片中基本二維葉型套用方法和沿葉高三維成型規律控制了葉片流道內部的流場，也決定了葉片的氣動性能。
對於基本二維葉型的設計，主要是儘可能地降低葉柵流動中的型面損失。前載入基本葉型（葉柵流道內的載荷主要集中在葉片的前緣區域，圖1中的（1））和後載入葉型（葉柵流道內的載荷主要集中在葉片的尾緣區域，圖1中的（2））在控制葉柵型面損失方面都達到了較高的水平。但總體來說，前載入葉柵在控制型面損失方面比後載入葉柵相對更有效（後載入葉型更難控制型線背弧上的擴壓程度），具有較小的型面損失。
對於葉片的三維成型設計，主要是將基本二維型線按照一定的扭轉規律和彎曲規律在葉片高度方向上積疊，從而實現對三維流場的有效控制。扭轉規律體現葉片的流型設計方法，彎曲規律反映葉片力對流場內參數分布的有效控制。
葉片三維成型後，在二維基本葉型固有的型面損失基礎上，葉柵流道內產生了複雜的三元流動，主要增加了端部區域（葉片根部葉高（圖2中的（3））和頂部葉高區域（圖2中的（5）））的二次流損失。2013年前，對於降低二次流損失的主要方法是：使用一種高度後載入基本型線，通過將型線的載荷轉移到尾緣附近，推遲二次流的產生，有效控制二次流動在通道內的發展，同時根據一定的型線模化、扭轉和彎曲規律，實現葉片的三維造型，從而有效控制葉片流道內的流場，降低流動損失。這種方法的主要不足是整個葉片沿葉高都採用一種高度後載入葉型，而對於沒有二次流流動影響或影響較小的葉片中部葉高區域，仍採用較難控制型面損失的高度後載入葉型，未對葉片型線載荷沿葉高的分布進行控制，最終可能導致中部區域的流動損失增加。
專利CN1982653A中提出了在同一個葉片中混合使用前載入葉型和後載入葉型的設計方法，即在葉片的根、頂部高度區域使用後載入葉型，最大程度控制二次流動損失，而在葉片中部高度區域（圖2中的（4））使用前載入葉型，最大程度降低型面損失。這種改變葉片載荷沿葉高分布規律的方法，可以同時利用前載入葉型和後載入葉型的優點，進一步降低總流動損失。但是，從另一方面講，專利CN1982653A僅僅提出了一種巨觀設計理念，並沒有提出更細節的設計方法，如葉型載荷沿葉高的分布規律具體是什麼形式、控制載荷的程度和控制範圍是多少等等，這在實際的工程設計中套用的可操作性並不強。
發明內容
專利目的
《透平葉片的載入方法》的目的在於：提供一種相對於2013年12月之前的技術更全面、更具體一種葉型載荷沿葉高的分布方法。
技術方案
《透平葉片的載入方法》所述透平葉片的二維葉型的載荷特性通過葉型的幾何參數UGT大小來控制，幾何參數UGT為：相鄰葉型內弧出口點到相鄰葉型背弧最短距離所在點對應的背弧上切線、與葉型背弧出口點處葉型背弧的切線之間的夾角；幾何參數UGT沿葉高的變化規律如下：
①當X＞0.45時，UGT1為常數，在16°~22°之間；
②當X＜0.05時，UGT2為常數，在4°~10°之間；
③當0.05≤X≤0.45時，在葉片根部區域（0，X）和頂部區域（1-X，1）的相對葉高範圍內，UGT3-1沿葉高以拋物線規律分布；
在葉片中部區域（X，1-X）的相對葉高範圍內，UGT3-2為常數，UGT3-2的值與上述UGT2相同。
所述UGT3-1沿葉高以拋物線規律分布數學模型如下：
其中，h-距離根部的高度，0＜h≤H。
有益效果
《透平葉片的載入方法》根據葉片的高度H和高寬比H/C（葉片高度H/葉片根部弦長C）來確定不同的載荷分配方法。葉片中二維葉型的載荷特性主要通過葉型的幾何參數UGT大小來控制，即通過控制二維葉型的幾何參數UGT沿葉高的變化規律，來得到葉片載荷沿葉高的分配規律。該發明明確了葉型載荷沿葉高的分布規律的具體情形、控制載荷的程度和控制範圍，在實際的工程設計中，利於大規模套用和推廣，操作性強。
附圖說明
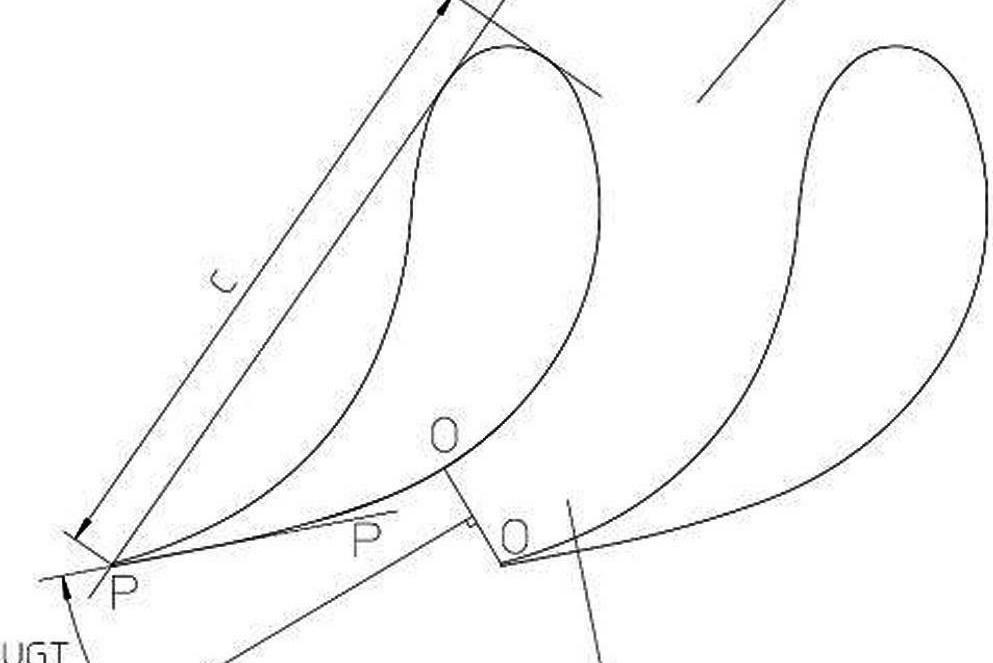
圖1為二維葉型幾何參數示意圖。
圖2為葉片根、中、頂區域示意圖。
圖3為X＞0.45時，葉片載荷沿葉高分布規律示意圖。
圖4為X＜0.05時，葉片載荷沿葉高分布規律示意圖。
圖5為0.05≤X≤0.45時，葉片載荷沿葉高分布規律示意圖。
圖中代號含義：1、平面葉柵流道內的前緣區域，2、平面葉柵流道內的尾緣區域，3、葉片根部高度區域，4、葉片中部高度區域，5、葉片頂部高度區域。
技術領域
《透平葉片的載入方法》涉及透平葉片的設計領域，主要指葉片型線的載荷沿葉高分布的控制方法：即根據葉片的高度H和高寬比（葉片高度H/葉片弦長C）來確定不同的載荷分布方法。
權利要求
1.《透平葉片的載入方法》其特徵在於：所述透平葉片的二維葉型的載荷特性通過葉型的幾何參數UGT大小來控制，幾何參數UGT為：相鄰葉型內弧出口點到相鄰葉型背弧最短距離所在點對應的背弧上切線、與葉型背弧出口點處葉型背弧的切線之間的夾角；幾何參數UGT沿葉高的變化規律如下：
①當X＞0.45時，UGT1為常數，在16°~22°之間；
②當X＜0.05時，UGT2為常數，在4°~10°之間；
③當0.05≤X≤0.45時，在葉片根部區域（0，X）和頂部區域（1-X，1）的相對葉高範圍內，UGT3-1沿葉高以拋物線規律分布；
在葉片中部區域（X，1-X）的相對葉高範圍內，UGT3-2為常數，UGT3-2的值與上述UGT2相同。
2.根據權利要求1所述的透平葉片的載入方法，其特徵在於：所述UGT3-1沿葉高以拋物線規律分布數學模型如下：
其中，h-距離根部的高度，0＜h≤H。
實施方式
如圖1～5所示，該發明是一種透平葉片的載入方法，指葉片型線的載荷沿葉高分布的控制方法，透平葉片的二維葉型的載荷特性通過葉型的幾何參數UGT大小來控制。幾何參數UGT為：相鄰葉型內弧出口點到相鄰葉型背弧最短距離（喉部位置）所在點對應的背弧上切線，與葉型背弧出口點處葉型背弧的切線之間的夾角，即葉型喉部位置線OO的垂直線與葉型背弧出口點切線PP之間的夾角。幾何參數UGT沿葉高的變化規律由葉片的高度H和高寬比H/C（葉片高度H/葉片根部弦長C）來確定，具體如下：
根據上式可以初步確定二次流動的影響區域，上式中的X代表根、頂部二次流動區域所占葉片總葉高的比重。因此：
①當X＞0.45時，UGT1為常數，在16°~22°之間；如圖3所示。
當X＞0.45時，表明二次流動所占比重較大，根、頂部區域的二次流動區域之和占總葉高的比重已經超過90%。此時，整個葉片高度內的二維葉型都可以使用一種後載入葉型，後載入程度可以通過葉型幾何參數UGT1確定，一般在16°~22°之間。
②當X＜0.05時，UGT2為常數，在4°~10°之間；如圖5所示。
當X＜0.05時，表明二次流動所占比重較小，根、頂部區域的二次流動區域之和占總葉高的比重不超過10%。此時，整個葉片高度內的二維葉型都可以使用一種前載入葉型，前載入程度可以通過葉型幾何參數UGT2確定，一般在4°~10°之間。
③當0.05≤X≤0.45時，僅使用一種前載入葉型或後載入葉型都無法最大程度減少流動損失，而合理改變葉型載荷沿葉高的分布規律可以達到同時控制二次流損失和減少型面損失的目的，如圖4所示，有兩種情況：
a、在葉片根部區域（0，X）和頂部區域（1-X，1）的相對葉高範圍內，UGT3-1沿葉高以拋物線規律分布；更進一步地，UGT3-1沿葉高以拋物線規律分布數學模型如下：
其中，h-距離根部的高度，0＜h≤H。b、在葉片中部區域（X，1-X）的相對葉高範圍內，UGT3-2為常數，UGT3-2的值與上述UGT2相同。這是符合載荷的具體分布規律的。
榮譽表彰
2017年12月11日，《透平葉片的載入方法》獲得第十九屆中國專利優秀獎。
