逆預測（Inverse prediction）也稱回歸控制、校準問題。當y對x的回歸模型根據樣本建立之後，先確定固變數y的某一取值y*，反過來去預測自變數x對應的取值x*及其區間。因這與通常的由自變數預測因變數的過程相反，故稱為“逆”預測。例如在生產中往往事先規定了產品的某種標準的水平，設計或研究人員要知道相應的工藝參數(自變數值)達到什麼水平，這就是逆預測問題。
基本介紹
- 中文名： 逆預測
- 外文名：Inverse prediction
- 別名：回歸控制、校準問題
- 所屬學科：數學（數理統計）
- 相關概念：回歸方程，回歸預測等
基本介紹,兩種情況,案例分析,
基本介紹
有些時候，要使用Y對X的回歸模型來預測給出了新觀察值Y的X的取值，這就是逆預測或統計控制。下面用兩個例子來說明。
1．某貿易聯合會分析人員對聯合會的15個企業進行回歸，研究某產品銷售價格(Y)與成本(X)之間的關係，如果已知不屬於這個貿易聯合會的某企業的銷售價格Yh(新)，要估計該企業的成本，Xh(新)。
2．以50個病例為基礎進行過某種新藥劑量(X)與類固醇減少水平(T)之間的回歸分析。某醫生正在治療一個新病人，要求把新病人的類固醇水平降到Yh(新)，他想估計出應給病人開的新藥劑量Xh(新)。
兩種情況
統計控制(statistical control)(或校準)就是利用Y對Xj的回歸方程，來預測給出新觀察值Y的Xj的取值，這就是逆預測問題。在給定
條件下，Xj估計值需分下面兩種情況來考慮。
1．若Y與Xj均為隨機變數，則預測和控制兩問題地位是平等的。於是可把應變數看作新自變數，而把原自變數看作新應變數，重新擬合線性回歸方程即可。
2．一般的控制問題，多用在自變數是非隨機變數的場合(實驗室、臨床試驗研究中多見)，因此不能像上面那樣反轉變數進行分析。這種情況下，預測和控制是兩個性質不同的問題。控制中，X雖未知，但是一個非隨機變數；而預測中，預測對象Y是隨機變數。
案例分析
回歸預測
如果回歸直線
經過檢驗，線性相關顯著，就可以用它來作變數的預測。對任一給定的
，相應的
一般是以回歸直線上對應值
為中心的服從常態分配的隨機變數，設這個隨機變數y的方差為
，則
。
此式表明，當
時，對應y值以0.95的機率落入區間
，這個區間稱為y的0.95預測區間，
稱為y的點預測值。
y的方差往往未知，但可以證明它的方差近似為
用S代替
，則對給定
機率為0.95的
預測區間為
。
一般為方便起見，近似取1.96為2，則上述區間近似為
，取
。
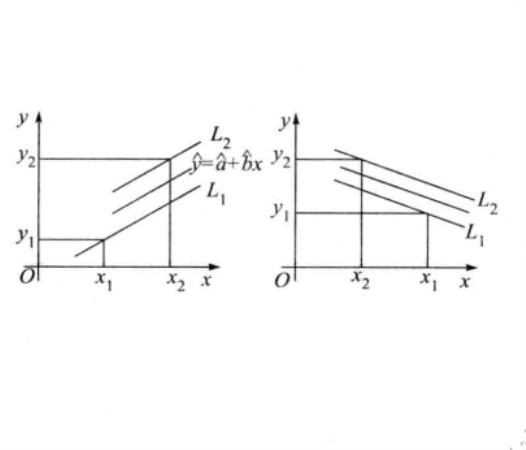
由於x值是變化的，因此y的預測區間上下限是平行於回歸直線的兩條直線
，如圖1(a)、(b)所示。
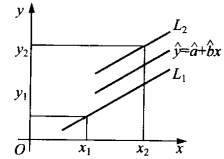圖1（a）
圖1（b）回歸控制
如果希望y落在區間
內，則x取值區間可由圖1中直線
對應關係確定。
設
設
解出
，則
當
時，控制區間為
；
當
時，控制區間為
。
但必須注意，只有當
時，所求控制區間才有意義。
