追逃對策(pursuit-evasion game)是雙方對追及與否的對策，一類典型的定性微分對策。參與對策的追、逃兩方，分別記為P和E，P方欲迫近E，E方相反，欲遠離P，若P方接近到E方的一定範圍，並用ψ(x)≤0(目標集)表示，則稱“追及”或“捕獲”，這時對策結束。
基本介紹
- 中文名：追逃對策
- 外文名：pursuit-evasion game
- 所屬學科：數學、運籌學
- 相關概念：微分對策、
基本介紹,詳細介紹,根本要素,局中人,策略,一局對策的得失,
基本介紹
追逃對策(pursuit-evasion game)是雙方對追及與否的對策，一類典型的定性微分對策。參與對策的追、逃兩方，分別記為P和E，P方欲迫近E，E方相反，欲遠離P，若P方接近到E方的一定範圍，並用ψ(x)≤0(目標集)表示，則稱“追及”或“捕獲”，這時對策結束。
目標集(termination set)是一種集合，是定性微分對策結束時所要求實現的集合。在定性微分對策中，對策結束時所要求實現的條件界定的集合，如用飛彈攔截飛機，要求在攔截過程結束時，飛機處於飛彈爆炸時能擊毀飛機的有效範圍內，亦即飛彈與飛機間的距離不超過某一給定值。一般地，目標集可寫成ψ(x)≤0。
詳細介紹
追蹤對策現象在軍事上是經常出現的，例如，殲擊機與轟炸機的戰鬥： 敵方的轟炸機要轟炸我方的目標，我方的殲擊機為保衛這些目標，必須在轟炸機進人目標的轟炸有效範圍之前打掉它或至少趕走它。此時，對策是由雙方駕駛員進行的。也有不是人直接指揮的追蹤對策，例如，反飛彈跟蹤彈道飛彈就是靠飛彈內部的自動控制裝置指揮的。在追蹤對策中追逃雙方是在空間或地面運動的。這裡逃的一方有時不是單純逃，而是企圖在被追到以前達到某種目的(例如達到有效轟炸的目的)。而追的一方就要在逃方達到那么，對於追蹤問題我們應該怎樣來研究呢? 微分對策提供了一種思路。讓我們來看一個有趣的例子。
構想有一隻老鼠在圓湖邊碰上了貓，它想回洞已來不及，只好跳人湖中企圖逃走。但貓在岸上跑的速度比鼠在湖中游的速度快得多,例如是鼠速的4 倍。粗看起來，老鼠沒有好辦法，只有束手就擒。但是，仔細研究一下，老鼠還是可以跑掉的。我們將老鼠所跑路線的奧妙介紹如下。
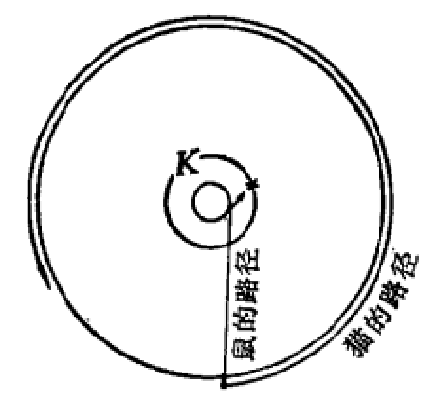
圖1圖1中大圓表示圓湖，其半徑設為R，取,
為半徑作一同心小圓K (我們將看到這是很有意思的區域)，於是老鼠跳人湖中後，先游到小圓K內，然後轉圈游，貓在岸上按圖中的路線跟著老鼠；但用同樣的時間，老鼠在圓K內轉圈所轉過的角度比貓沿湖岸轉圈轉過的角度要大。所以老鼠可以游到和貓不在同一半徑，而在同一直徑的圓K的邊界點*的位置上去，然後沿此直徑游向湖岸。因為*點到湖岸的最短距離是
設鼠的速度為v，則鼠由*點到湖岸所需的時間是
由於貓的位置同*點不在同一半徑上，所以貓到達同一地點的路程正好是半圓周，即
。那么，貓的速度雖是鼠的4 倍(即4v)，但貓所需時間是
，而
，所以鼠先上岸，且有時間迅速跑入附近的鼠洞而溜掉。因此鼠確實有逃掉的辦法，此也即為鼠的最優策略。所以發現這個有意思的小圓很重要。自然會問，對於一般追蹤問題，存不存在這樣或那樣的有意思的區域呢? 同樣會問，各種初始情況下，追逃雙方的最優策略是什麼? 微分對策的理論，就是提供一些思路來幫助人們找到這些問題的答案。
根本要素
追蹤問題也存在對策現象所共有的根本要素：
局中人
此時局中人就是追者與逃者，例如在空戰中是一方的殲擊機和另一方的轟炸機，在空防中是攻方的轟炸機和守方的高射炮，在飛彈戰中是一方的飛彈和另一方的反飛彈等等。
策略
追逃雙方都有自己的可選擇的行動方案，例如轟炸機可選擇飛行路線和投彈方式等，殲擊機可選擇迎擊時間，飛行路線和攻擊方式等，高射炮可選擇發射角度等等。不過在追蹤問題中局中人的完整的行動方案(即所謂策略)比矩陣對策中的完整的行動方案要複雜得多了。因為在追蹤問題中，局中人例如殲擊機必須每時每刻都掌握雙方的相對位置和某些情況以便跟蹤追擊。同樣轟炸機也得每時每刻都能掌握雙方的相對位置和某些情況以便躲過攻擊，飛達轟炸目標。所以用數學描述追蹤對策中的策略，也必須要反映出這種連續動態的決策過程。這就得藉助微分方程的理論，因此這類對策理論稱為微分對策。
在微分對策中,通常用向量X(t)表示時刻t 時各方為繼續進行對策所必須知道的雙方的狀況的量，例如空戰中雙方飛機的相對位置和機頭所指方向等等，因此X(t)也被稱為狀況變數。
同時，各局中人都有控制自己運動路線的手段，例如飛機駕駛員可以做改變機速和使機頭拐彎等操作，於是機速和機頭拐彎的曲率半徑等是屬於局中人直接可控的量，這些量的改變就能引起前述狀況變數的改變，並且這些量將怎么變，對方是不知道的，所以這些量稱做控制量。
於是局中人的一個策略就是決定一個連續控制的規律,即對任意狀況變數X(t) 給出自己應選的控制量。所以控制規律就是狀況變數的函式，記為
(對追者)，
(對逃者)。
一般，當控制規律
為各方選定以後，雙方的運動情況可由某個微分方程組描述：
從理論上說，當給定了初始狀況
和控制規律後，由運動方程可解出雙方在這局對策中自始至終的運動路線。
一局對策的得失
對於追蹤對策，當追著了或逃掉了，即到達運動路線的終點時，這局對策也就結束了。但在終點上的得失不光是追著或逃掉，因為有時逃者並非單純逃，而是企圖在被追到以前達到某種目的。那么，追者必須在逃者達到目的之前追著它才是最好的。所以數學上應根據雙方的目的，對得失(下面稱作支付)作出不同的描述。例如：
(1) 如果關心的是能否追著，那么支付就可以用追著的時間來描述，沒追著就對應於追著時間為無窮大或大於某個時刻T(即追者因動力燃料限制不能無限追下去)。支付這樣描述時，追者是要儘快追著，即極小化追著的時間，而逃者則要極大化追著的時間。
(2) 如果關心的是進不進入某目標的鄰域，那么支付可用追著時離目標鄰域的距離來描述。此時保衛此目標者要極大化此距離，而襲擊此目標者則要極小化這個距離。
總之在追蹤問題中，對得失作出恰當的量的描述之後，總是一方要極大化這個量，而另一方則要極小化這個量。所以，在追蹤問題中以極大極小原則定義最優策略，也是很令人信服的。
解決這一類問題，可運用連續函式的運動學微分方程求解：
式中
為追方的控制函式關係，
為逃方的控制函式關係，X是描寫追逃雙方相互位置的狀態變數。若能給定初條件，則可解該方程以求得雙方的運動路線。
