迴路電壓定律

迴路電壓定律，即基爾霍夫電壓定律。基爾霍夫電壓定律(Kirchhoff laws)是電路中電壓所遵循的基本規律，是分析和計算較為複雜電路的基礎，1845年由德國物理學家G.R.基爾霍夫（Gustav Robert Kirchhoff，1824～1887）提出。

內容是，在任何一個閉合迴路中，各元件上的電壓降的代數和等於電動勢的代數和，即從一點出發繞迴路一周回到該點時，各段電壓的代數和恆等於零，即∑U=0

基本介紹

• 中文名：迴路電壓定律
• 外文名：Kirchhoff Voltage Law
• 別稱：基爾霍夫電壓定律
• 表達式：Eu=0
• 提出者：G.R.基爾霍夫
• 提出時間：1845年
• 套用學科：物理
• 適用領域範圍：電路基礎

簡介

基爾霍夫(電路)定律是求解複雜電路的電學基本定律。在19世紀40年代，由於電氣技術發展的十分迅速，電路變得愈來愈複雜。某些電路呈現出網路形狀，並且網路中還存在一些由3條或3條以上支路形成的交點 (節點)。這種複雜電路不是串、並聯電路的公式所能解決的，剛從德國哥尼斯堡大學畢業，年僅21歲的基爾霍夫（Gustav Robert Kirchhoff，1824～1887），1845年，在他的第1篇論文中提出了適用於這種網路狀電路計算的兩個定律，即著名的基爾霍夫定律。該定律能夠迅速地求解任何複雜電路，從而成功地解決了這個阻礙電氣技術發展的難題。

基爾霍夫定律包括基爾霍夫第一定律和基爾霍夫第二定律，其中基爾霍夫第一定律稱為基爾霍夫電流定律，簡稱KCL；基爾霍夫第二定律即為基爾霍夫電壓定律，簡稱KVL。因此，這裡介紹的迴路電壓定律是基爾霍夫第二定律。

定律

電壓定律內容

基爾霍夫電壓定律表明：

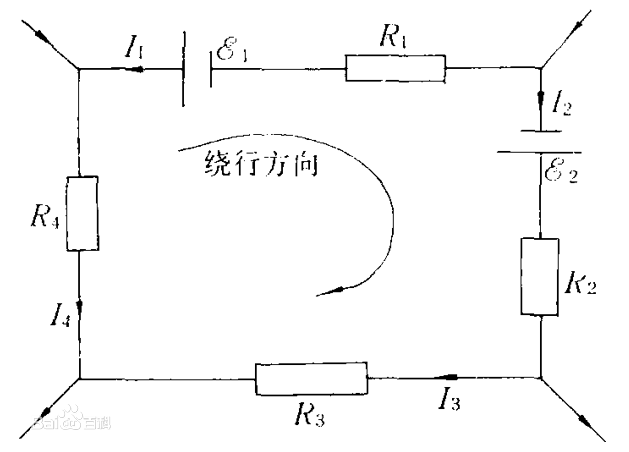
1. 如果從迴路中任意一點，以順時針方向或逆時針方向沿迴路循行一周，則在這個方向上的電位降之和應等於電位升之和.即：U升=U降
   
2. 在任一瞬間，沿任意迴路的循行方向（順時針方向或逆時針方向）， 迴路中各部分電壓的代數和恆等於零。書中規定：凡電動勢的參考方向與所選迴路循行方向一致者取“負”，相反者則取“正”； 凡電流參考方向與迴路循行方向一致者，該電流在電阻上所產生的電壓降取“正”，不一致者則取“負”。即
   

說明：電源電動勢的參考方向———物理學中規定，從電源負端經電源內部指向電源正端的方

向為電源電動勢的參考正方向.

3.在任一迴路的循行方向上，迴路中電動勢的代數和應等於迴路中各電阻上電壓降的代數和。書中規定：凡電動勢的參考方向與所選迴路循行方向一致者取“正”，相反者則取“負”；凡電流參考方向與迴路循行方向一致者，該電流在電阻上所產生的電壓降取“正”，不一致者則取“負”。即

等效表達

電路中某兩點間的電壓應等於由起點到終點間任意一條路經上各部分電壓降的代數和。強調：在所選擇的路徑上，某部分電壓降低，則取“正”；某部分電壓升高，則取“負”其數學表達式為：

Uab=U1降+U2降+…+Un降+U1升+U2升+…+Un升。

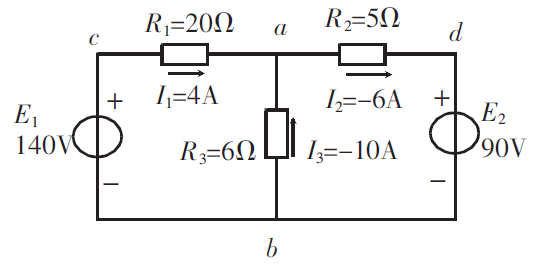
舉例套用

例1 如圖2 所示，已知：E1=140V，E2=90V，R1=20Ω，R2=5Ω，R3=6Ω，I1=4A，I2=-6A，I3=-10A， 選

擇三條路徑分別求出Uab。

例題迴路

解：依據“基爾霍夫迴路電壓定律的“等效表述”分別得到Uab。

選擇acb 路徑：

Uab=-I1R1+E1=-4×20+140=60V；

選擇adb 路徑：

Uab=I2R2+E2=(-6)×5+90=60V；

選擇ab 路徑：

Uab=-I3R3=-(10)×6=60V。

可見：由a 到b，無論選擇那一條路徑，計算出Uab的值都是60V