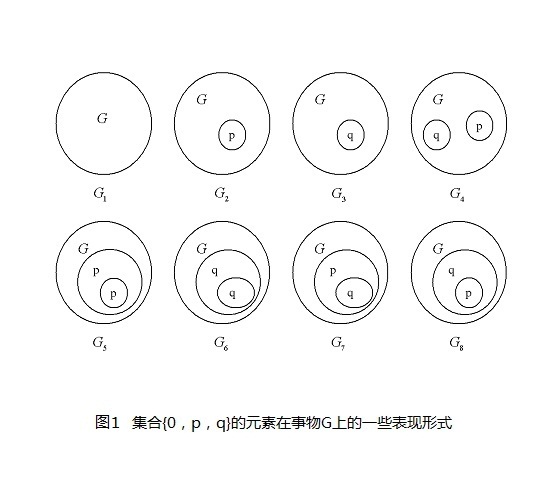
辯證代數是一種描述辯證法的代數。在文獻[1]里,我們可以看出辯證代數是和布爾代數十分相似的。布爾代數的集合里基本常量是0和1,即用0表示假,1表示真;其運算符號分別有與運算、或運算和非運算,分別用符號“·”“+”“-”來表示。而辯證代數的基本常量集合是{0,p,q},其中0表示無,p和q均表示有,但p和q表示任意一種關係的辯證矛盾的兩極,例如p表示真,q表示假;或例如p表示是,q表示否。但是p不能表示男,q不能表示女,因為p和q只能表示為一種可以變化的關係,該關係的辭彙通常是形容詞,而男和女是名詞。在辯證代數裡,它只有兩種運算,一種是“甲和乙同時在一件事物上表現”,“…同時在”用符號“+”來表示;另一種是“甲在乙之上表現,其表現所給出的結果再在某一件事物上表現”,“…在…之上”用符號“·”來表示。在辯證運算里,要先算“·”再算“+”,符號“·”在運算的時候可以省略。
原理一的建立,原理二的建立,辯證代數成為純數學的可能,
原理一的建立
根據文獻[1],當所有辯證矛盾的變化都只表現為雙極相互轉化而不表現為單極遞變時,任何事物的表現都只能是集合{0,p,q}的元素組合,且任何事物的表現都只能是0、p、q或p+q,所以它有如下一組原理等式:
1. 0+0=0, p+p=p, q+q=q;
2. 0+p=p+0=p, 0+q=q+0=q;
3. p+q=p+q+p=q+p+q=q+p。
上面這些原理等式對於“…同時在”顯而易見是成立的,稱之為原理一。
原理二的建立
文獻[1]里說到,由於矛盾是對立統一的,所以p在q上的表現其實相當於自身在自身上表現,則p·q=q·p,即對於{0,p,q}內元素的“·”運算,其交換律成立。又p和q的變化只表現為相互轉化,所以p和q的變化結果只能是p或q,所以p在q上的表現所獲得的結果為p·q=p或p·q=q。由於矛盾的表達具有對稱性,所以在運算的時候我們可以選擇是p·q=p成立,而不選擇p·q=q。
另外,如果有和無是一對辯證矛盾,那么無是可以在任何東西上表現的,這個表現必然會導致一種存在出現,這個出現必然屬於一種有,是一種事物。而在任何一種事物里,其內在的辯證矛盾都是辯證統一的,所以文獻[1]認為無在無之上表現,其實是衍生了一對對的其它辯證矛盾,即0·0=p+q。
然後,假如令p=0,q=1(這裡的1表示為有),那么根據前面的p·q=p易得0·1=0,該假設驗算成立。反之,假如令p=1,q=0,那么根據p·q=p則得0·1=1,這假設是和前面的0·0=p+q相背的,因為p+q就是一種有,相當於1,所以這一個假設不成立。則根據0·1=0得:
0·p=p·0=0·q=q·0=0,於是進而可推導出
0·0=(0·p)·(0·q)=(0·0)·(p·q)=(p+q)·p,根據“…同時在”的含義,其分配律顯然成立,則有
(p+q)·p=p·p+q·p=0·0=p+q,即有p·p+p=p+q,所以有p·p=q。然後又進行推理如下
q·q=q·(p·p)=(q·p)·p=p·p=q,於是又得出了q·q=q。
有了上面那些結論之後,文獻[1]就將之歸納成了一組原理等式,稱之為原理二:在{0,p,q}里設p·q=p,則以下等式成立:
4. p·q=q·p=p;
5. p·p=q·q=q;
6. 0·0=p+q, 0·p=p·0=0·q=q·0=0。
根據上面的原理二,我們就很容易得出“真·真=真”,“真·假=假”,“假·假=真”,這就包含了否定之否定規律的意義。至於為什麼“假·假=真”,這是因為假在自己身上表現,自己否定了自己是假(這種說法其實有點籠統,我們還可以參照文獻[1]里的那種推理方法,即在“真·真=真”里由於前一個真在後一個真之上的表現不發生作用變化,所以後一個真的表現結果在事物上表現仍然為真,則在“假·假=真”里,必然有前一個假在後一個假之上的表現發生作用變化,後一個假的變化由於只存在相互轉化這種變化,所以後一個假只能向真轉化),則其在自己身上表現的結果,這個結果在其它事物上表現就為真了。其它的辯證矛盾諸如正負、進出(這裡的進出已經被規定了只能是相互轉化,所以沒有半進半出的概念,半進半出說的是進或出的程度,已經具有了辯證矛盾單極遞變的概念,單極遞變是不符合辯證代數的前提條件的)等也類似於這樣解釋。
辯證代數成為純數學的可能
根據原理一和原理二,對於辯證代數的變數x、y、z的運算,顯然,我們有如下運算律:
(一)交換律 x+y=y+x, x·y=y·x ;
(二) 結合律 (x+y)+z=x+(y+z), (x·y)·z=x·(y·z) ;
(三) 分配律 x·(y+z)=x·y+x·z ;
由於辯證代數的交換律、結合律、分配律均成立,所以辯證代數作為一種純數學理論而存在是可能的。實際上,從單純定義上來說,即把原理一和原理二看成一種定義,看成一種公理約定,辯證代數的運算系統都是自洽的。既然自洽,有什麼理由不能成為一種數學呢!
另一方面,辯證代數從另一角度其實也給出了數學中“正數·正數=正數”、“正數·負數=負數”及“負數·負數=正數”的哲學解釋,而除此之外,數學算術的這些等式的哲學解析是十分模糊的,它們的解釋通常只能使用例子,但例子的解釋是不全面的,甚至“負數·負數=正數”我們根本就無法用例子來作出解釋。如果說辯證法是解析所有哲學及科學的基礎的話,那么將辯證法進行形式化或數學化之後,它仍然應該有此功能的,而一些人運用數理邏輯將辯證邏輯進行形式化之後[2],我們根本就找不出其這樣的功能,顯然他們的做法是失敗的;或者那種照著辯證法三大規律(對立統一規律、量變質變規律、否之否定的規律)而任意套用符號所給出的形式化,例如文獻[3],由於它們不存在數學般的那種演繹功能,則他們的做法也是失敗的。