轉彎半徑(RADIUS OF TURNING CIRCLE),是指汽車行駛過程中,由轉向中心到前外轉向輪與地面接觸點的距離。
基本介紹
- 中文名:轉彎半徑
- 外文名:RADIUS OF TURNING CIRCLE
簡介
最小轉彎半徑
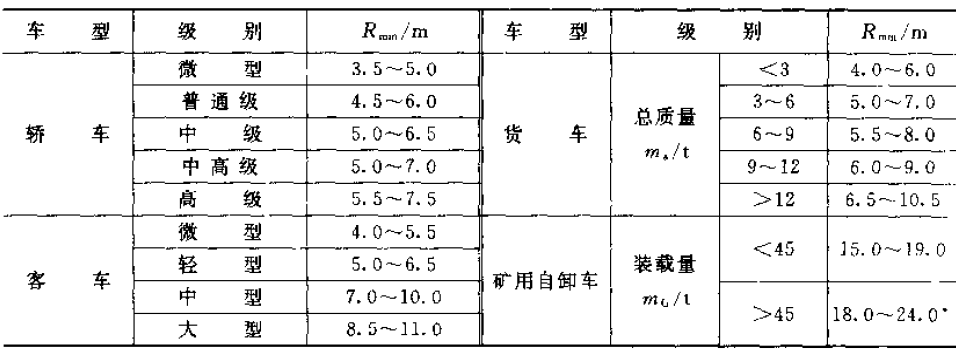 表1 各種汽車最小轉彎半徑
表1 各種汽車最小轉彎半徑阿克曼轉向幾何
 圖2 阿克曼轉向幾何
圖2 阿克曼轉向幾何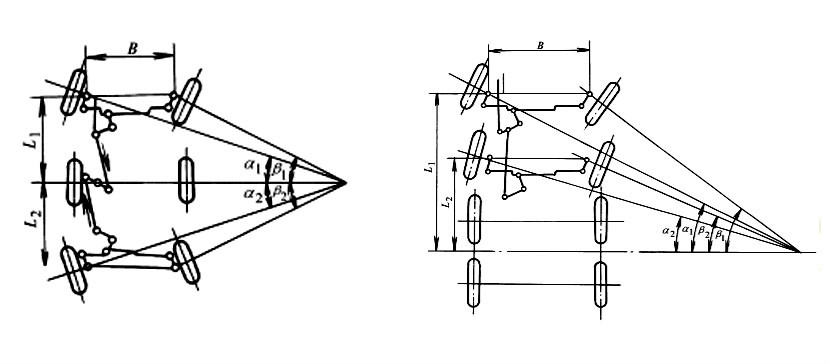 圖3 多軸汽車阿克曼轉向幾何
圖3 多軸汽車阿克曼轉向幾何
轉彎半徑(RADIUS OF TURNING CIRCLE),是指汽車行駛過程中,由轉向中心到前外轉向輪與地面接觸點的距離。
 表1 各種汽車最小轉彎半徑
表1 各種汽車最小轉彎半徑 圖2 阿克曼轉向幾何
圖2 阿克曼轉向幾何 圖3 多軸汽車阿克曼轉向幾何
圖3 多軸汽車阿克曼轉向幾何轉彎半徑(RADIUS OF TURNING CIRCLE),是指汽車行駛過程中,由轉向中心到前外轉向輪與地面接觸點的距離。...
最小轉彎半徑是指當轉向盤轉到極限位置,汽車以最低穩定車速轉向行駛時,外側轉向輪的中心在支承平面上滾過的軌跡圓半徑。它在很大程度上表征了汽車能夠通過狹窄彎曲...
道路轉彎半徑是公路專業的術語,也叫曲線,曲線一般又有圓曲線和緩和曲線,或單圓曲線或組合。單圓曲線半徑比較大,也是就是直線和圓的相切點。...
在國標操穩六項試驗的“穩態迴轉”試驗中,根據記錄的橫擺角速度及汽車前進速度,用下式計算各點的轉彎半徑及側向加速度。Ri=Vi/ri,其中Ri為 第i 點轉彎半徑,m...
汽車最小轉彎半徑(Minimumturn radius of car)是指,當轉向盤轉到極限位置,汽車以最低穩定車速轉向行駛時,外側轉向輪的中心平面在支承平面上滾過的軌跡圓半徑。...
最小曲線半徑是鐵路上常用的技術標準,非專業的場合也稱為‘轉彎半徑’,其意義等於幾何學上的曲線半徑。這個數字的倒數能夠反映曲線的彎曲程度,即曲率。在鐵路上提到...
轉彎率是指飛機飛行航向的瞬時改變或者穩態改變率,反映飛機的方向機動性。轉彎率,其單位通常是度每秒,它的大小決定於設定的空速和坡度。只要其中一個參數發生改變,...
轉彎諸元是指轉彎時飛行速度、轉彎坡度、轉彎半徑、轉彎時間和轉彎率的總稱。飛機按一定飛行速度形成轉彎後,由於坡度使升力減小,出現掉高度的現象。因此,必須抬頭或...
程式轉彎,起始進近航跡和最後進近航跡方向相反的一種機動飛行。飛行中先進行轉彎脫離指定航跡,然...程式轉彎可分兩種:①45°/180°程式轉彎,先按指定航跡平飛一...
同時道路盡頭設定回車場時,回車場面積應根據汽車最小轉彎半徑和路面寬度確定,消防道路最小轉彎半徑6m(內徑)能滿足消防車的最小轉彎要求了。...
有適宜的航道轉彎半徑航道轉彎半徑是指航道中心線上的最小曲率半徑。一般航道轉彎半徑不得小於最大航行船舶長度的4-5倍。若河流轉彎半徑過小,將造成航行困難,應加...
貨櫃車指將密封箱式貨櫃固定在汽車底盤上的運輸車輛。貨櫃車的轉彎半徑數據之一:貨櫃車40呎貨櫃車轉彎半徑為18米,供貨櫃車行駛的道路內轉彎半徑要小於18米。...
最小轉彎半徑 6.3m 6.3m 6.3m 6.3m 6.3m 驅動方式 前輪驅動 前輪驅動 前輪驅動 前輪驅動 前輪驅動 乘員人數(含司機) 整備質量 1720kg 1740kg 1740kg 18...
內輪差(Difference of Radius Between Inner Wheels)是車輛轉彎時內前輪轉彎半徑與內後輪轉彎半徑之差。對汽車列車,則是牽引車的內前輪與掛車的內後輪轉彎半徑之差...
汽車的軸距短,汽車長度就短,質量就小,最小轉彎半徑和縱向通過半徑也小,汽車的機動性就好。但如果軸距過短,則車廂長度就會不足,後懸 (車輛最後輪軸線與汽車最...
最小轉彎半徑 5.2m 5.2m 5.2m 5.2m 5.2m 5.2m 5.2m 5.2m 驅動方式 前輪驅動 前輪驅動 前輪驅動 前輪驅動 前輪驅動 前輪驅動 前輪驅動 前輪驅動...
最小轉彎半徑 6.3m 6.3m 6.3m 6.3m 6.3m 驅動方式 前輪驅動 前輪驅動 前輪驅動 全時四驅 全時四驅 乘員人數(含司機) 整備質量 1800kg 1820kg 1820kg ...
