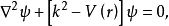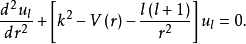輳力場

輳力場又稱有心力場。對場中任意位置上的質點的作用力恆通過場中某一固定點的力場。此固定點稱為該輳力場的力心。指向力心的場力稱為引力；背向力心的場力稱為斥力。

基本介紹

• 中文名：輳力場
• 外文名：A central force field
• 又稱：有心力場
• 套用：輳力場是物理學中極為重要的力場
• 套用學科：量子力學術語
• 範疇：數理科學

概念

輳力場是物理學中極為重要的力場。質點和密度分布是點至球心距離的函式的球體所產生的萬有引力場，就是它的最常見的特例。在輳力場中，質點只受到通過力心的場力的作用，因而質點對力心的角動量守恆（見角動量守恆定律），質點被限制在它的初速度矢量和力心所構成的平面內運動，且以力心為原點的矢徑在單位時間內掃過的面積為常數，即面積速度為常數，它等於質點初始時刻對力心的角動量的一半。
如輳力場的場力的大小隻依賴於質點至力心的距離 ，而和質點在力場中的方位無關,即場力式中 為單位矢量，這樣的輳力場必為保守力場（見保守力），因而具有勢能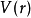 。質量為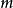 的質點以速度 在這樣的力場中運動時，質點的機械能守恆。

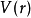
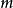
輳力場中的彈性散射

在輳力場的情況下，勢能 只與粒子到散射中心的距離 有關，與 的方向無關。方程寫為

取沿粒子入射方向並通過散射中心的軸線為極軸，這個軸是我們所討論問題中的旋轉對稱軸，波函式 和散射振幅 都與 角無關。

方程的一般解可寫為

現在 既與 無關，所以 ，因而 的一般解寫為

這個展式中每一項稱為一個分波， 是第 個分波，每一個分波都是方程的解。通常稱的分波分別為分波。徑向函式滿足下列方程：

令

則滿足方程