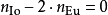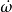簡介
軌道共振是天體力學中的一種效應與現象,是當在軌道上的天體於周期上有簡單(小數值)的整數比時,定期施加的引力影響到對方所產生的。軌道共振的物理原理在概念上類似於推動兒童盪的鞦韆,軌道和擺動的鞦韆之間有著一個自然頻率,其它機制和“推”所做的動作周期性的重複施加,產生累積性的影響。軌道共振大大的增加了相互之間引力影響的機構,即它們能夠改變或限制對方的軌道。在多數的情況下,這導致“不穩定”的互動,在其中的兩者互相交換動能和轉移軌道,直到共振不再存在。在某些情況下,一個諧振系統可以穩定和自我糾正,所以這些天體仍維持著共振。例如,木星衛星佳利美德、歐羅巴、和埃歐軌道的1:2:4共振,以及冥王星和海王星之間的2:3共振。土星內側衛星的不穩定共振造成土星環中間的空隙。1:1的共振(有著相似軌道半徑的天體)在特殊的情況下,造成太陽系大天體將共享軌道的小天體彈射出去;這是清除鄰居最廣泛套用的機制,而此一效果也套用在目前的行星定義中。
除了拉普拉斯共振圖中指出,共振比率應被解釋為在相同的時間間隔內完成軌道數的比例,而不是作為公轉周期比(其中將會呈反比關係)。上面2:3的比例意味著在冥王星完成兩次完整公轉的時間,海王星要完成三次完整的公轉。
歷史
自17世紀發現牛頓萬有引力定律以來,從拉普拉斯開始,就有許多數學家全神貫注太陽系的穩定性。二體問題近似解的穩定軌道忽略其它天體的影響。在太陽系中添加其它天體的相互作用對穩定性造成的影響很小,但是首先不知道在很長的周期中添加會造成何種軌道參數的改變和不同的配置,或是其它一些穩定的影響是否能維持行星軌道的配置。
拉普拉斯是最先找到解釋伽利略衛星奇異舞蹈(見下文)答案的人。持平而論,自當時迄今以來,在這個領域的研究是非常活躍的,但是仍有許多待解決的問題(例如,在巨大行星的環,環中的小衛星和微粒的相互作用如何維繫環)。
共振的類型
通常,軌道共振可能

涉及一個或任何組合的軌道參數(例如,離心率相對於半長軸,或軌道傾角)。
從短期的任何時間尺度來看,在10至10年的長期測量都有其通約性。
導致即使長期穩定運行的軌道,也有可能造成不穩定性。
平均運動軌道共振發生在兩個天體的公轉周期,其中一個的周期是對方的簡單整數比。依據詳細的的資料,這可以使軌道穩定,也可以使軌道被摧毀。當這兩個天體在這種同步的運動中沒有密切接觸時,可能會出現穩定。例如:
無論與海王星多么接近,冥王星和冥族小天體的軌道都是穩定的,因為它們與海王星是3:2的共振。共振可以確保當它們接近近日點和海王星的軌道時,海王星是在相當遠的距離之外(平均有它的軌道距離的四分之一)。其它沒有共振的近海王星天體(數量更多)會被海王星強大的攝動從這個區域逐出。還有規模較小,但是很明確有著1:1共振的共振海王星外天體(海王星特洛伊)、3:5(周期約275年)、4:7(周期約290年)、1:2(周期約330年)、和2:5(周期約410年),除此之外,在海王星之外還有其它的。
在距離太陽3.5AU以內的小行星帶,有與木星有著3:2、4:3、和1:1的族群分布著(特別是希爾達族、(279)圖勒、和特洛伊天體)。
軌道共振也可以摧毀一個穩定的軌道。對小天體而言,不穩定實際上是更有可能的。例如:
在距離太陽3.5AU以內的小行星帶,與木星的主要平均運動軌道共振落在小行星位置分布的空隙,柯克伍德空隙(最顯著的是在3:1、5:2、7:3、和2:1的共振)。在這些位置上的小行星因為反覆的受到木星的攝動,幾乎已經完全被拋空了。然而,還是有少數的小行星目前暫時在或接近這些共振的位置。例如,艾琳達族就為位於或接近3:1共振,而它們的軌道離心率在與木星的相互作用下持續的在增加,直到最終它們會與內側的行星密切接觸,然後將它們從共振軌道彈射出去。
在土星環內,卡西尼縫是B環和外側的A環之間的空隙,與米瑪斯有著2:1的共振(更特別的是卡西尼縫內側邊緣惠更斯縫的位置。)。
在土星環,恩克環縫和基勒環縫是與置身在A環內的潘和達佛涅斯1:1共振清空微粒形成的。A環的外側是由土衛十有著7:6的不穩定共振維繫著。
大多數天體中的共振軌道都有著相同的方向,然而有少數是逆行的,達摩克型小行星是被土星或木星捕獲,並被發現暫時處在平均運動軌道共振上的小行星。這種軌道的相互作用比軌道在同一方向的機制的相互作用為弱。
拉普拉斯共振發生在三個或更多天體的軌道周期之間有著簡單整數比的系統上。例如,木星的佳利美德、歐羅巴、和埃歐軌道的1:2:4軌道共振。系外行星格利澤876e、b、和c,也有1:2:4的軌道共振。
林達博共振導出螺旋密度波不僅適用在星系(恆星是受螺旋臂本身的力支配的),也適用於土星環(環中的微粒是受到土星衛星的力支配)。
長期共振發生於兩個軌道的進動同步時(通常是近日點或升交點)。一顆小天體在與大許多的天體(例如行星)長期共振下,將有與大天體相同的速率。長時間(100萬年或更長)的長期共振會改變小天體的軌道離心率和軌道傾角。
幾個明顯的長期共振例子,包括土星都是。土星自轉軸的進動和海王星自轉軸的進動之間有著共振(兩者的周期都長達187萬年),已經確定與土星巨大的轉軸傾角(26.7°)可能有著相同的來源。最初,土星的傾角大概是比角接近木星(3.1°)。古柏帶逐漸的枯竭使海王星的進動減少;最終,兩著的頻率匹配,而土星的軸向進動進入到自旋-軌道共振,導致土星的傾角增加(海王星軌道的角動量是土星自轉的10倍,因此主導著互動的關係。)。
小行星和土星之間的拱點長期共振(ν6=g -g6)協助塑造出了小行星帶。接近它的小行星,離心率會緩慢的增加,直到它們成為接近火星的小行星。此時,它們會因為與火星遭遇而從小行星帶彈出。這種共振形成小行星帶內部和側面邊界的距離大約是2AU和約20°的軌道傾角。
數值模擬認為水星和木星(g1=g5)之間的拱點長期共振,最終有可能增加水星的離心率,並且可能在今後的數億年破壞內太陽系。
在土星環C環內的泰坦小環代表著另一種形式的共振,在其中的一個軌道的拱點進動率完全符合另一個的公轉速度。這個偏心小環外側的末端永遠朝向土星最大的衛星泰坦。
古在共振發生在對軌道傾角和離心率攝動的同步振盪(增加離心率而同時漸少傾角,反之亦然)。這種共振僅適用於高軌道傾角的天體;因此,這種軌道往往是不穩定的,因為越來越大的離心率會導致近心點變小,因而造成碰撞或被潮汐力破壞(對於大衛星)。
涉及軌道離心率另一種類型的例子是木衛三和木衛四的離心率,即使有著相對的相位,依然有181年的共通變化周期。
在太陽系的平均運動共振
在太陽系內只有少數的平均運動共振,包括行星、矮行星或大的天然衛星是已經知道的(在小行星、行星環、小衛星和更小的古柏帶天體,和許多可能的矮行星還會有更多):
2:4忒堤斯–米瑪斯(土星的衛星)
2:3冥王星–海王星
1:2狄俄涅–恩克拉多斯(土星的衛星)
3:4許珀里翁–泰坦(土星的衛星)
1:2:4佳利美德–歐羅巴–埃歐(木星的衛星)
此外,妊神星被認為是與海王星有著7:12的共振,鬩神星和鳥神星與海王星分別有5:17和6:11的共振。
周期之間簡單的整數比之後,很方便和簡化的隱藏了許多更複雜的關係:
參考稍後的插圖,考慮埃歐-歐羅巴著名的1:2共振。如果軌道周期在這種的關係,平均運動
(周期的倒數,通常表示為度/每天)將滿足下式:
代入資料(來自維基百科)將可以得到−0.7395° /日,於零有著極大不同的值!
實際上,共振是完美的,但它也涉及近木點(軌道上最接近木星的點)的進動
。正確的方程(拉普拉斯方程的一部分)是:
換言之,在考慮到近木點的進動,埃歐的平均運動確實是歐羅巴的兩倍。一位者設定在漂移的近木點上的觀測者,將看見衛星距角在同一個地點伸展。除了忒堤斯–米瑪斯,列在上面的其它對都滿足相同類型的方程。在這種情況下,共振滿足方程
天秤動的會合點將會圍繞在這兩顆衛星交點的中間點上。
拉普拉斯共振
最著名的共振涉及埃歐-歐羅巴-佳利美德,包括下面鎖定衛星軌道相位的關係:
此處
是衛星的平均經度。這種關係使得三重的合是不可能的。圖解說明了衛星埃歐在1、2、和3個周期後的位置。(在格利澤876的系統,相較之下,是最外層行星的運行軌道和每一顆行星合的三重關係。)
冥族小天體的共振
矮行星冥王星被困在與海王星有著共振軌道的圈套中,他的共振包括:
這些共振的一個結果是當冥王星越過海王星的軌道時,兩者之間的距離至少在30天文單位以上,而兩者之間最小的距離大約是17天文單位,而冥王星和天王星之間的距離最小距離只有11天文單位。(詳細的解釋和圖說請參見冥王星的軌道。)
同樣和海王星有著2:3共振的天體,稱為冥族小天體,是可能成為矮行星的亡神星。亡神星的軌道離心率和傾角都與冥王星相似,然而與海王星有著相同的共振使它很不自然的總在與冥王星相對的相位上;所以亡神星有時會被描述為反冥王星。
系外行星的平均運動共振
雖然大多數以經被發現的系外行星系統還沒有被發現有平均運動共振,但已有一些明顯的例子被揭漏:
如前述題道的格利澤876e、b和c,有著1:2:4的軌道共振,周期分別為124.3、61.1和30天。
KOI-730d、b、c和e出現3:4:6:8的共振,軌道周期為19.72、14.79、9.85和7.38天。
KOI-500c、b、e、d和f,出現接近20:27:41:62:193的共振,周期分別為9.522、7.053、4.645、3.072和0.9868天。
KOI-738和KOI-787出現一對7:9共振的行星(比率各自為1/1.285871和1/1.284008)
克卜勒37d、c和b出現誤差在1%內的5:8:15共振,周期分別為39.792187、21.301886和13.367308天。
系外行星中呈現接近1:2共振平均運動的現象非常普遍。凌日法發現的系統有16%的報告中有這樣的事例(周期比例的範圍在1.83-2.18)。以都卜勒光譜特徵發現的系外行星系統也有六分之一的比例(在這種情況下周期比率的範圍更窄)。由於對系統的知識還不完整,實際的比例可能會更高。整體而言,約三分之一徑向速度系統的特徵有一對行星接近通約性。更常見的視一對行星的軌道周期有著接近平均運動共振的比率,不是高了幾個百分點就是低了幾個百分點(特別是在第一階的共振,整數上的比率只有一個有不同)。在與恆星有潮汐作用的情況下,這樣的預測是很接近真實的。
符合'接近'比率的平均運動
在行星或主要衛星之間的軌道頻率有時會指出有接近整數數值的比率關係(見下面的清單)。然而,這並沒有任何動力學上的意義,因為沒有適當的近日點進動或其它振動使共振更為完美(詳細的討論參見前節的敘述)。即使這種不匹配相當的小(不同於真正的共振),這種接近共振的動態還是無意義的,因為在每個周期後,這些天體的相對位置還是會偏移。在天文學的短時間尺度平均值,它們相對的位置是隨機的,就像完全不靠近共振狀態的機構。例如,考慮地球和金星的軌道,它們在金星公轉13周和地球公轉8周之後,又配置在軌道上幾乎相同的對位置上。正確的比率是0.61518624,和精確的8:13隻有0.032%的偏差。在8年後,金星在軌道位置上的偏移只有的1.5°。不過,這依然可以讓金星和地球經過120個循環後,也就是960年後,發現彼此在對面的位置上。因此,在數千年或更長時間尺度上(以天文學的標準仍然很小),它們的相對位置實質上依然是隨機的。
一些軌道頻率的巧合包括:
| (比率)和天體 | 一個循環後的偏差 | 隨機化時間 | 或然率 |
|---|
(9:23)金星−水星 | 4.0° | 200y | 0.19 |
(8:13)地球−金星 | 1.5° | 1000y | 0.065 |
(243:395)地球−金星 | 0.8° | 50,000y | 0.68 |
(1:3)火星−金星 | 20.6° | 20 y | 0.11 |
(1:2)火星−地球 | 42.9° | 8 y | 0.24 |
(1:12)木星−地球 | 49.1° | 40 y | 0.28 |
(2:5)土星–木星 | 12.8° | 800 y | 0.13 |
(1:7)天王星−木星 | 31.1° | 500 y | 0.18 |
(7:20)天王星−土星 | 5.7° | 20,000 y | 0.20 |
(5:28)海王星−土星 | 1.9° | 80,000 y | 0.052 |
(1:2)海王星−天王星 | 14.0° | 2000 y | 0.078 |
(1:4)Deimos−Phobos | 14.9° | 0.04 y | 0.083 |
(1:1)智神星−穀神星 | 1.2° | 700 y | 0.0066 |
(7:18)木星−智神星 | 4.1° | 4000 y | 0.15 |
(17:45)Romulus−Remus | 0.7° | 40 y | 0.067 |
(1:6)Io−Metis | 0.6° | 2 y | 0.0031 |
(3:5)Amalthea−Adrastea | 3.9° | 0.2 y | 0.064 |
(3:7)Callisto−Ganymede | 0.7° | 30 y | 0.012 |
(2:3)Enceladus−Mimas | 33.2° | 0.04 y | 0.33 |
(2:3)Dione−Tethys | 36.2° | 0.07 y | 0.36 |
(3:5)Rhea−Dione | 17.1° | 0.4 y | 0.26 |
(2:7)Titan−Rhea | 21.0° | 0.7 y | 0.22 |
(1:5)Iapetus−Titan | 9.2° | 4 y | 0.051 |
(3:4)天王星−(10199)Chariklo | 4.5° | 10,000 y | 0.073 |
(3:5)Rosalind−Cordelia | 0.22° | 4 y | 0.0037 |
(1:3)Umbriel−Miranda | 24.5° | 0.08 y | 0.14 |
(3:5)Umbriel−Ariel | 24.2° | 0.3 y | 0.35 |
(1:2)Titania−Umbriel | 36.3° | 0.1 y | 0.20 |
(2:3)Oberon−Titania | 33.4° | 0.4 y | 0.34 |
(1:20)Triton−Naiad | 13.5° | 0.2 y | 0.075 |
(1:2)Proteus−Larissa | 8.4° | 0.07 y | 0.047 |
(5:6)Proteus−S/2004 N 1 | 2.1° | 1 y | 0.057 |
| 58.5° | 0.2 y | 0.33 |
| 39.1° | 0.3 y | 0.22 |
| 9.2° | 2 y | 0.05 |
| 6.6° | 3 y | 0.037 |
| 42.5° | 2 y | 0.55 |