基本介紹
- 中文名：軌道傾角
- 外文名：英語：Orbital inclination
- 領域：天文學
軌道,其他意義,計算,
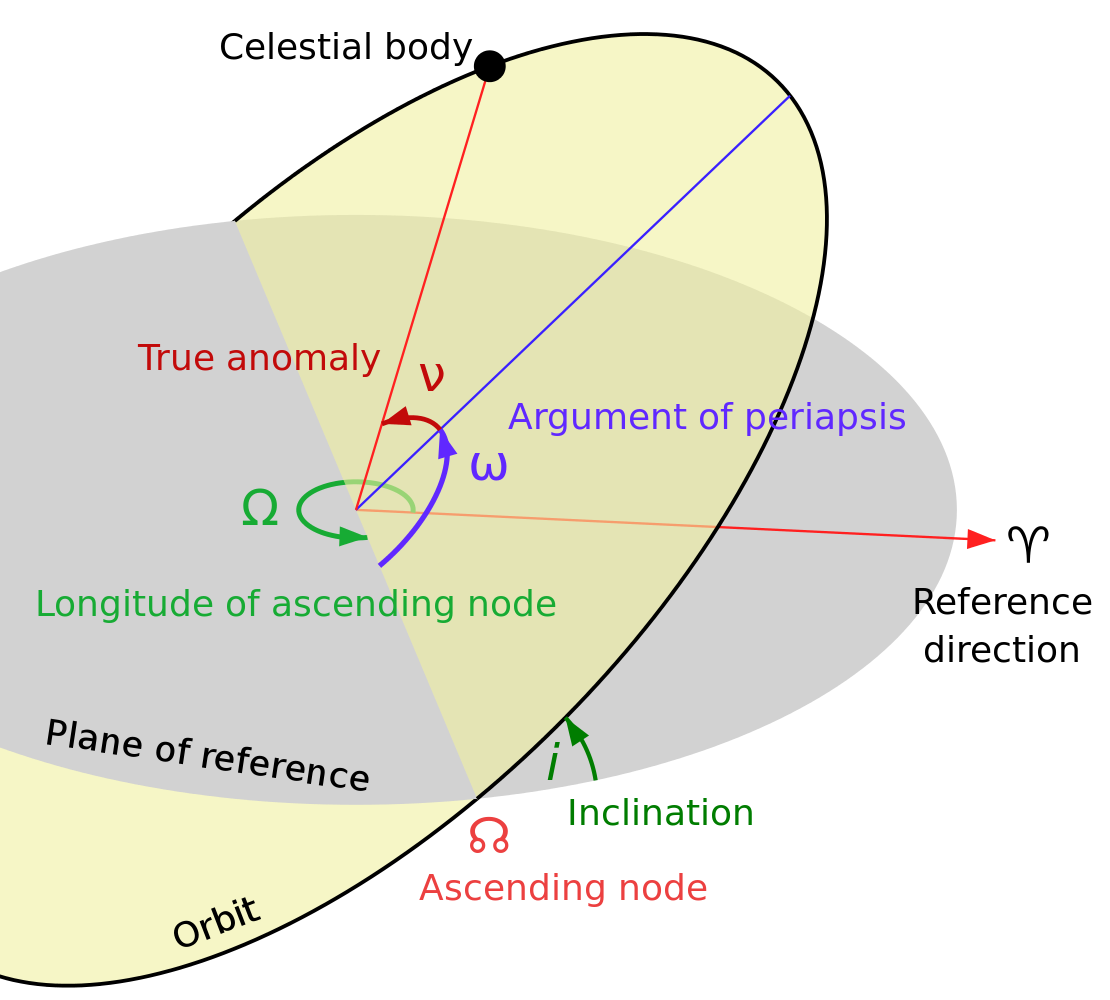
軌道
明確的說，傾角是描述天體軌道的形狀和方向的六個軌道要素之一。它是行星的軌道平面和參考平面（通常以黃道或赤道為主）之間的角距離，並以角度來描述。
在太陽系，行星軌道的傾角被定義為行星的軌道平面和黃道——地球繞太陽軌道所位於的平面——的角距離。它也可能以另一個平面來測量，例如太陽的赤道或木星的軌道平面，但對地球上的觀測者來說，黃道面是最實用的。大部分在太陽系內的行星軌道平面對彼此之間和太陽赤道的傾角都很小。比較值得注意的例外是矮行星中的冥王星和鬩神星，他們的傾角分別是17度和44度；還有小行星中的智神星傾角為34度。目前已知的許多系外行星，在多行星系統中也有一些是高傾角的。
衛星或人造衛星的傾角，如果與行星的距離夠近，就會以它們所環繞的行星赤道面來測量，赤道平面是垂直於自轉軸並通過中心的平面。
（1）傾角0度的意義是環繞物體的軌道就在行星的赤道平面上，並且與行星運行的方向一致；例如： 地球靜止軌道衛星(GEO星)
（2）傾角90度是繞極的軌道，太空船會經過行星的南極和北極，另外；
（3）傾角180度是在赤道平面上逆行的軌道。
如果物體離中心的天體很遠，就需要使用另一種參考平面：拉普拉斯平面。在遠離主星時，拉普拉斯平面從赤道平面分離開來，偏移的角度越來越大，直到與主星的軌道平面有最大的角距離。
對一個自轉軸的方向不知道或是不明確的天體，一顆衛星的將以黃道面為量測的參考，有時（對移動緩慢的天體）會相對於天空的平面（參看下面對聯星的定義）。
對月球，他的傾角是相對於地球的赤道平面，這導致他的數值變化迅速且變數很大，因此相對於黃道來測量會比較合理（這意味著月球是和地球一起繞著太陽轉的），而且幾乎就是一個常數值。
| 軌道傾角 | 名稱 | 黃道傾角 | 太陽赤道傾斜 | 不變平面傾角 |
|---|---|---|---|---|
| 類地行星 | ||||
水星 | 7.01° | 3.38° | 6.34° | |
金星 | 3.39° | 3.86° | 2.19° | |
地球 | 0 | 7.155° | 1.57° | |
火星 | 1.85° | 5.65° | 1.67° | |
| 氣態行星 | ||||
木星 | 1.31° | 6.09° | 0.32° | |
土星 | 2.49° | 5.51° | 0.93° | |
天王星 | 0.77° | 6.48° | 1.02° | |
海王星 | 1.77° | 6.43° | 0.72° |
其他意義
*對行星和其它運轉中的天體，自轉軸的傾角是法線和軌道平面的角度，但使用轉軸傾角（ axial tilt）或傾斜度 （ obliquity）意義會更加明確。
*明確的說，對地球而言，對黃道的傾斜度是黃道面和赤道面之間的角度。
*對在太陽系外天體的傾角，像是聯星，因為沒有其它的可以做為參考，就被定義為軌道平面（也就是軌道的軸）的法線與觀測者方向所夾的角度。同樣的，這也可以視為軌道平面和天空平面之間所夾的角度，因為後者也是依據觀測者所住視的方向定義出來的，所以在比較天球上不同區域的恆星時要格外的小心。當聯星的傾角接近90度（側向時）經常會互食 。
計算
在太空動力學，軌道傾角，可以由下式算出：
i=arccos hz/|h|
此處：
hz是h在Z-方向上的分量。h是垂直於軌道平面的軌道角動量向量。
