軌跡線性化控制(Trajectory Linearization Control,TLC) 方法是一種基於微分代數譜理論的非線性控制方法,在NASA先進制導控制項目中被成功套用於X-33的上升段姿控系統設計。TLC方法的設計思想是:首先利用非線性動態逆方法將軌跡跟蹤問題轉化為一個跟蹤誤差調節問題,然後利用線性時變系統PD譜理論設計狀態反饋控制律, 使得該誤差跟蹤系統一致漸近穩定。
基本介紹
- 中文名:軌跡線性化控制
- 外文名:Trajectory Linearization Control
- 簡稱:TLC
- 學科:控制科學與工程
- 套用:制導
- 基本釋義:基於微分代數譜理論的非線性控制
基本概念,TLC方法的設計思想,結構,LQR與TLC在制導中的套用比較,
基本概念
軌跡線性化控制(Trajectory Linearization Control,TLC) 方法是一種基於微分代數譜理論的非線性控制方法,在NASA先進制導控制項目中被成功套用於X-33的上升段姿控系統設計。
TLC方法的設計思想
在多數控制問題中,設計控制器的目的是希望被控對象的狀態或輸出在控制律的作用下跟蹤期望的標稱指令,在飛控問題中就是要求飛行器的姿態能夠快速準確地跟蹤制導系統發出的姿態角命令。TLC方法的設計思想是:首先利用非線性動態逆方法將軌跡跟蹤問題轉化為一個跟蹤誤差調節問題,然後利用線性時變系統PD譜理論設計狀態反饋控制律, 使得該誤差跟蹤系統一致漸近穩定。控制器結構如圖1所示。
圖1

考慮如下形式的多輸入多輸出非線性系統:

定義如下的狀態跟蹤誤差:

並構造控制律為:
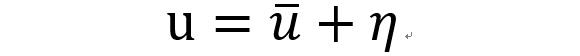
其中,η即為所需設計的線性時變反饋控制律。則對應的非線性跟蹤誤差動態系統為:
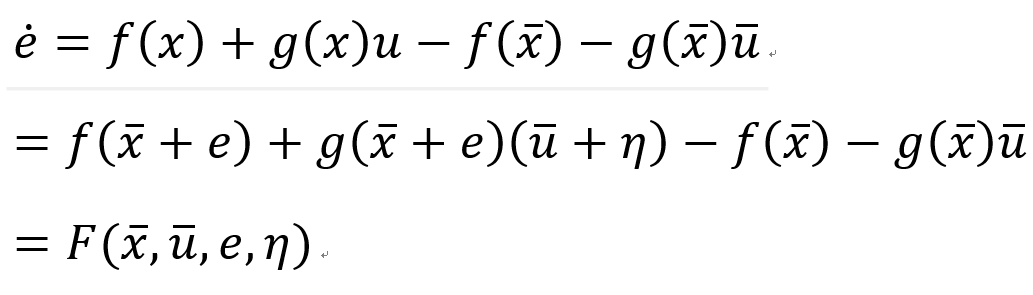
此時,原非線性系統跟蹤問題就轉化為一個非線性調節問題,控制器包括兩部分:
(1)一個開環的被控對象的偽動態逆控制器, 根據期望的系統輸出值 y產生一個標稱的控制輸入 u;
(2)一個閉環的線性時變反饋調節器η=η(e)用以鎮定系統, 並使系統具有一定的回響特性。
結構
TLC(其概念如圖2所示)結構由兩部分組成:通過非線性模型偽逆求得給定標稱輸出η(t)對應的標稱控制量μ(t) ,以粗略對消系統的非線性,並將一般的軌跡跟蹤問題轉化為在誤差坐標系的狀態調節問題,上方帶“-”的變數為變數的標稱值; 將非線性時變誤差動力學方程組線性化,通過李雅普諾夫坐標變換將一般的線性時變方程組轉化為線性時變系統標準型,並通過配置Parallel Differential Spectrum(PD譜)對誤差動態進行鎮定。反饋控制項μ(t)由時變鎮定控制器產生,並可寫為狀態誤差量的線性反饋形式μ(t)=K(t)ξ(t)。
TLC 對跟蹤誤差信號可以保證指數穩定性,閉環系統對正則擾動及奇異攝動都有很好的適應性。
圖2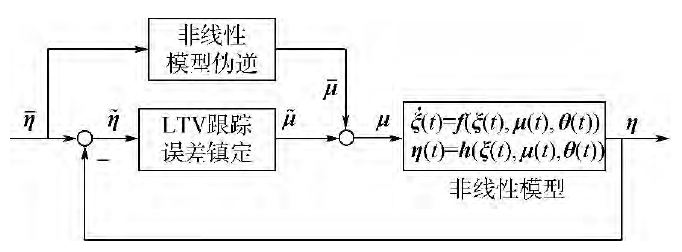

LQR與TLC在制導中的套用比較
線性二次型調節器( Linear Quadratic Regulator,LQR) 控制由於反饋增益可以採用誤差狀態的線性反饋控制律構成最優閉環,設計時能夠考慮允許的狀態偏差和控制量偏差等多個指標,在參數不確定的情況下閉環系統也具有一定魯棒性,在多入多出系統的控制方面獲得了較多套用。
與LQR方法相比,TLC方法具有更寬的適應範圍,其原因在於基於LQR的增益調度方法需要求解Riccati方程,通常難以實時求得最優反饋增益,一般只能根據設計好的參考軌跡離線計算獲得後存儲於制導計算機。為了適應不同的參考軌跡,只能在地面離線生成多組增益,套用時需要根據實際採用的參考軌跡來選用對應的制導反饋增益。由於設計中通常無法考慮所有的非理想情形,因此採用這類制導律設計具有潛在的風險。而TLC方法不依賴於參考軌跡,反饋增益可以符號化表示為參考軌跡的函式,並只需計算簡單的代和增益大小與無量綱自然頻率直接相關;對於參考軌跡的不同階段或差別較大的參考軌跡,通過線上改變不同環路自然頻率的數值(同時保證環路間頻寬的分離)即可實現期望的控制效果;另外,TLC方法需要調整的參數數量很少且調整的方向性非常明確。這些區別使得TLC方法不僅可以適應更寬範圍的再入飛行制導任務,而且與軌跡線上生成算法一起將可極大提高再入制導的自主性,適應於應急再入任務規劃、線上任務改變或落點調整等情形。
(1)TLC方法在初始狀態拉偏和擾動情況下也能實現很高的跟蹤精度,體現了方法的有效性和魯棒性。
(2)與LQR方法的仿真結果相比,TLC需要調整的參數更少,參數的選取更直觀,對不同參考軌跡有很好的適應性,是一種完全線上的非線性控制方法。與近似滾動時域控制相比,TLC在控制精度略優於前者的情況下計算量顯著減小。
(3)在再入軌跡跟蹤制導律中使用TLC控制,可以做到制導環和姿態環控制結構的統一和設計時的一體化;高度、速度、姿態角和姿態角速度的四環路TLC控制策略將更便於制導和控制參數的匹配和實時調整。
因此,TLC跟蹤制導策略對於減少制導指令的解算時間,提高制導的自主性、適應性和精度有一定工程意義。

