跳表:簡介,原理,理想情況,實例,級的分配,性能分析,時間複雜性,空間複雜性,跳表

跳表

增加了向前指針的鍊表叫作跳表。跳表全稱叫做跳躍表，簡稱跳表。跳表是一個隨機化的數據結構，實質就是一種可以進行二分查找的有序鍊表。跳表在原有的有序鍊表上面增加了多級索引，通過索引來實現快速查找。跳表不僅能提高搜尋性能，同時也可以提高插入和刪除操作的性能。

基本介紹

中文名：跳表
外文名：Skip list
全稱：跳躍表
類型：隨機化的數據結構
實質：可以進行二分查找的有序鍊表
優點：提高搜尋，插入和刪除性能

簡介,原理,理想情況,實例,級的分配,性能分析,時間複雜性,空間複雜性,跳表的實現,

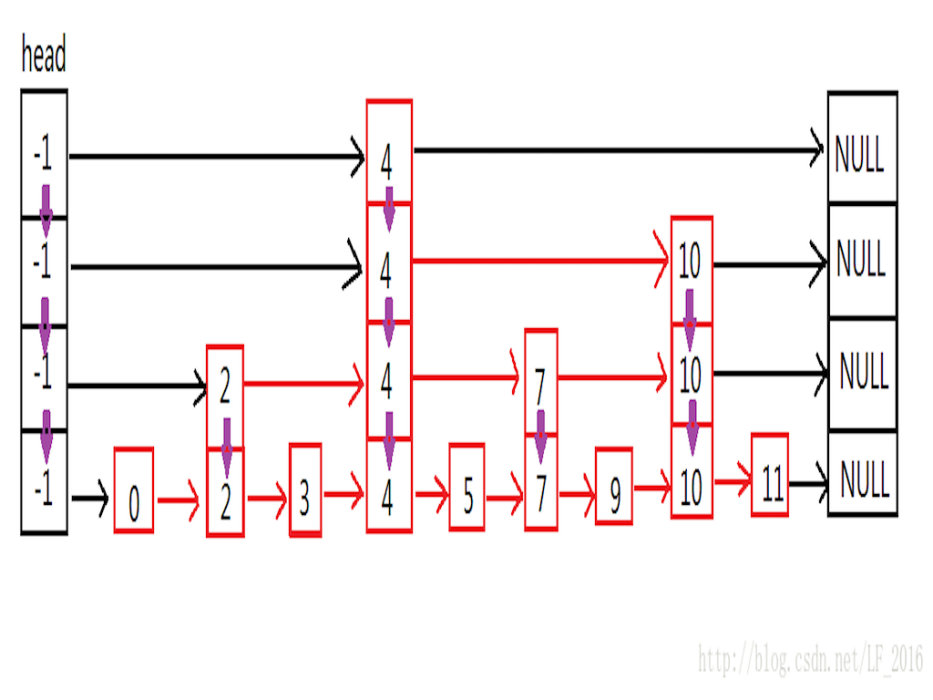
簡介

跳表是一個隨機化的數據結構，可以被看做二叉樹的一個變種，它在性能上和紅黑樹，AVL樹不相上下，但是跳表的原理非常簡單，目前在Redis和LeveIDB中都有用到。

它採用隨機技術決定鍊表中哪些節點應增加向前指針以及在該節點中應增加多少個指針。跳表結構的頭節點需有足夠的指針域，以滿足可能構造最大級數的需要，而尾節點不需要指針域。

採用這種隨機技術，跳表中的搜尋、插入、刪除操作的時間均為O(logn)，然而，最壞情況下時間複雜性卻變成O(n)。相比之下，在一個有序數組或鍊表中進行插入/刪除操作的時間為O(n)，最壞情況下為O(n)。

原理

跳表的原理非常簡單，跳表其實就是一種可以進行二分查找的有序鍊表。跳表的數據結構模型如圖1:

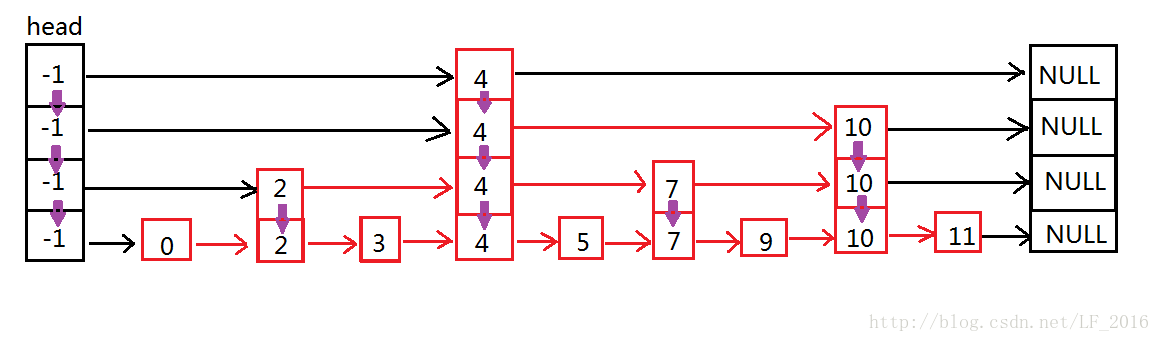
圖1數據結構模型

可以看到，跳表在原有的有序鍊表上面增加了多級索引，通過索引來實現快速查找。首先在最高級索引上查找最後一個小於當前查找元素的位置，然後再跳到次高級索引繼續查找，直到跳到最底層為止，這時候以及十分接近要查找的元素的位置了(如果查找元素存在的話)。由於根據索引可以一次跳過多個元素，所以跳查找的查找速度也就變快了。

理想情況

在一個使用有序鍊表描述的具有n個元素的字典中進行搜尋，至多需進行n次比較。如果在鏈中部節點加一個指針，則比較次數可以減少到n/2+1。搜尋時，首先將欲搜尋元素與中間元素進行比較。如果欲搜尋的元素較小，則僅需搜尋鍊表的左半部分，否則，只要在鍊表右半部分進行比較即可。

實例

圖2中c所示的結構為跳表（skiplist）。在該結構中有一組有層次的鏈。0級鏈是包含所有元素的有序鍊表，1級鏈是0級鏈的一個子集。i級鏈所包含的元素是i-1級鏈的子集。圖2c中，i級鏈上所有的元素均在i-1級鏈上。

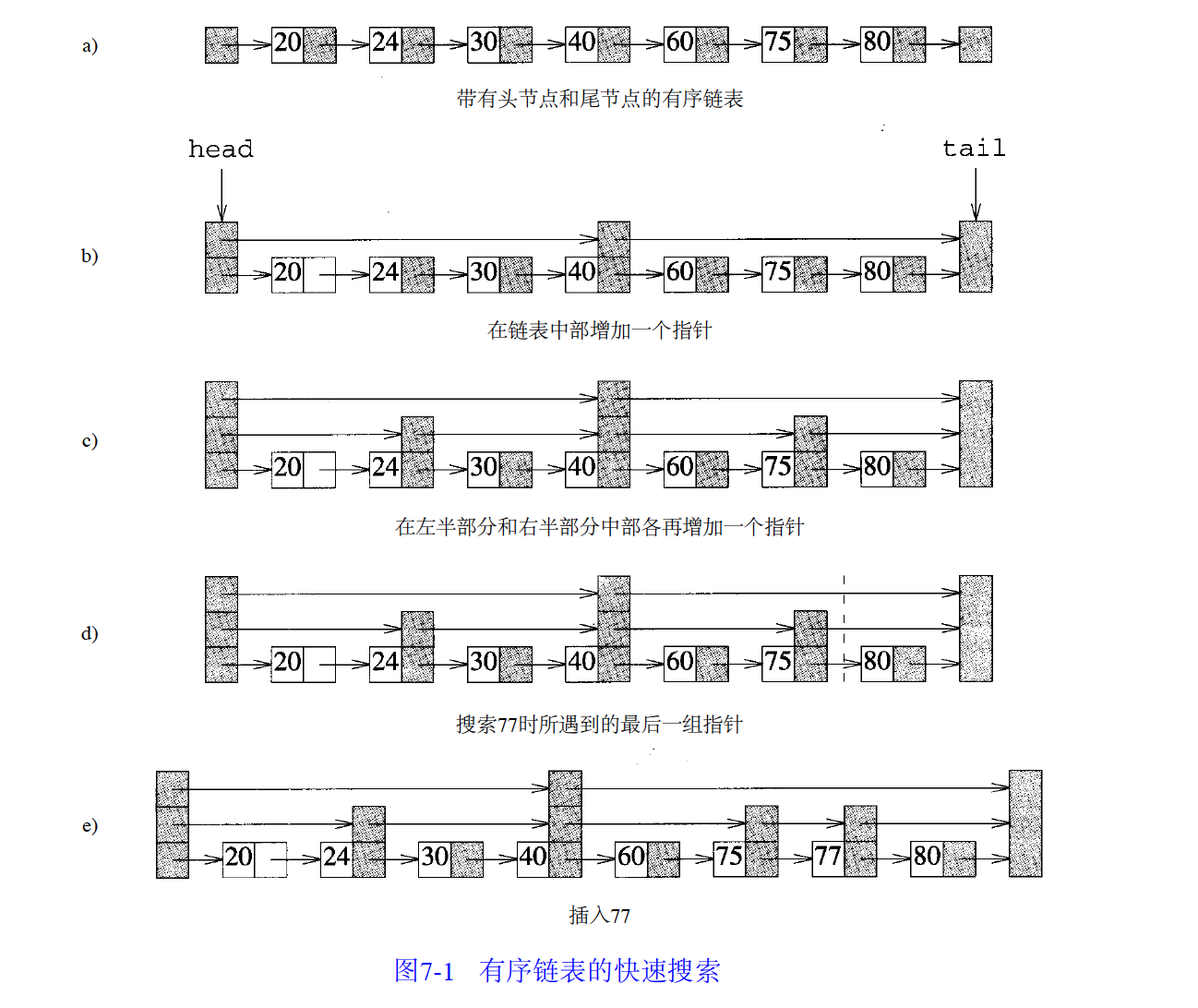
圖2有序鍊表的快速搜尋

如圖2的有序鍊表中有七個元素。該鍊表有一個頭節點和一個尾節點。節點中的數是該節點的值。對該鍊表的搜尋可能要進行七次比較。可以採用圖2b中的辦法，把最壞情況下的比較次數減少為四次。搜尋一個元素時，首先將它與中間元素進行比較，然後根據得到的結果，或者與鏈的左半部比較或者與右半部比較。例如如果要找值為26的元素，只需查找40左邊的元素。如果要查找值為75的元素，那么只對40以後的元素進行搜尋即可。

也可以向圖2c中一樣，分別在鍊表左半部分和右半部分的中間節點再增加一個指針，以便進一步減少最壞情況下的搜尋比較次數。在圖2中有三條鏈。0級鏈就是圖2a中的初始鏈，包括了所有七個元素。一級鏈包括第二，六個元素，而2級鏈只包括第四個元素。為了尋找值為30的元素，首先與中間元素比較。在2級鏈中尋找元素所需要的時間為(1)。由於30<40，因此要搜尋該鏈左半部分的中間元素。採用1級鏈進行搜尋所花費的時間為(1)。又因為30>24，故需在0級鏈中繼續進行查找，把該元素與鏈中下一個元素進行比較。

級的分配

在級基本的分配過程中，可以觀察到，在一般跳表結構中，i-1級鏈中的元素屬於i級鏈的機率為p。假設有一隨機數產生器所產生的數在0到RANDMAX間。則下一次所產生的隨機數小於等於CutOff=p*RANDMAX的機率為p。因此，若下一隨機數小於等於CutOff，則新元素應在1級鏈上。現在繼續確定新元素是否在2級鏈上，這由下一個隨機數來決定。若新的隨機數小於等於CutOff，則該元素也屬於2級鏈。重複這個過程，直到得到一隨機數大於CutOff為止。故可以用下面的代碼為要插入的元素分配級。

intlev=0;

while(rand()<=CutOff) lev++;

這種方法潛在的缺點是可能為某些元素分配特別大的級，從而導致一些元素的級遠遠超過log_1/pN，其中N為字典中預期的最大數目。為避免這種情況，可以設定一個上限lev。在有N個元素的跳表中，級MaxLevel的最大值為

可以採用此值作為上限。

另一個缺點是即使採用上面所給出的上限，但還可能存在下面的情況，如在插入一個新元素前有三條鏈，而在插入之後就有了10條鏈。這時，新插入元素的為9級，儘管在前面插入中沒有出現3到8級的元素。也就是說，在此插入前並未插入3，4，⋯，8級元素。既然這些空級沒有直接的好處，那么可以把新元素的級調整為3。

性能分析

時間複雜性

當跳表中有n個元素時，搜尋、插入、刪除操作的複雜性均為O(n+MaxLevel)。在最壞情況下，可能只有一個MaxLevel級元素，且餘下的所有元素均在0級鏈上。i>0時，在i級鏈上花費的時間為(MaxLevel)，而在0級鏈上花費的時間為O(n)。儘管最壞情況下的性能較差，但跳表仍不失為一種有價值的數據描述方法。其每種操作(搜尋、插入、刪除)的平均複雜性均為O(logn)，

空間複雜性

至於空間複雜性，注意到最壞情況下所有元素都可能是MaxLevel級，每個元素都需要

MaxLevel+1個指針。因此，除了存儲n個元素(也就是n*sizeof(element))，還需要存儲鏈指針（所需空間為O(n*MaxLevel)）。不過，一般情況下，只有n*p個元素在1級鏈上，n*p₂個元素在2級鏈上，n*p_i在i級鏈上。因此指針域的平均值(不包括頭尾節點的指針)是n/(1-p)。因此雖然最壞情況下空間需求比較大，但平均的空間需求並不大。當p=0.5時，平均空間需求(加上n個節點中的指針)大約是2n個指針的空間。

跳表的實現

#ifndef _SKIPLIST_H__
#define _SKIPLIST_H__
#include<time.h>
#include<iostream>
#include<vector>
#include<cstdio>
#include<cstdlib>using namespace std;
#define MAXLEVE 8                                             //跳表的最大層數
template<typename K,typename V>struct SkipNode                                               //跳表的節點類型{   K _key;               V _value;     size_t _sz;                                                //表示該節點的層數   vector<SkipNode<K,V> *> _pleve;                            //存放每一層的指針   SkipNode(K key=K(),V value=V(),size_t sz=size_t())               :_key(key)        ,_value(value)        ,_sz(sz)    {        _pleve.resize(0);        for(size_t i=0;i<sz;i++)        {            _pleve.push_back(NULL);        }    }   ~SkipNode()   {        _key=-1;        _value=-1;        _sz=-1;        _pleve.clear();   }};
template<typename K,typename V>class SkipList                       //跳表類
{
public:
    typedef SkipNode<K,V> Node;    SkipList();
    void Insert(K key,V value);
    bool Find(K key,V& value);    
    bool Erase(K key);    
    void Print();    
    int GetLeve();                                            //返回跳表的最大層數    size_t Size();    ~SkipList();private:    int Random();                                             //產生隨機層數的函式protected:                                          SkipList(SkipList<K,V> &);                                //防拷貝    SkipList<K,V>& operator=(SkipList<K,V>);                  //防賦值private:    Node *_head;    
    int _maxLeve;                                            //記錄跳表的最大層數    int _size;                                                //記錄跳表最底層元素的個數};

跳表