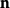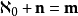基本介紹
- 中文名：超限數
- 外文名：transfinite numbers
- 人物：康托爾
- 領域：數理科學
- 概念：超過所有的有限數的數字
- 別稱：無窮大數
簡介,含義,
簡介
超限數的研究是根據數學理論發展的需要提出來的，自從1883年德國數學家康托爾(1829 一1920) 建立集合 論以來，集合論的思想和方法已經滲透到各個領域。在數學研究對象中，更多的是無窮集合，用什 么 樣 的 數刻 劃無窮集合元素個數的無窮程度成了研究無窮集合的一個重要問題。十九世紀末期 ，康托爾首先進行了超限數的 研究，基本上解決了這一 問題，使超限數的思想和方法成了今日數學的基礎。
超限數是大於所有有限數（但不必為絕對無限）的基數或序數。分別叫做超窮基數和超窮序數。
術語“超限”（transfinite）是康托爾提出的，他希望避免詞語無限（infinite）和那些只不過不是有限（finite）的那些對象有關的某些暗含。當時其他的作者少有這些疑惑；現在被接受的用法是稱超限基數或序數為無限的。但是術語“超限”仍在使用。
超窮序數可以確定超窮基數，並導出阿列夫數序列。
含義
1.最小超限序數是ω。
2.第一個超限基數是aleph-0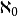
，整數的無限集合的勢。如果選擇公理成立，下一個更高的基數是aleph-1
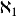。如果不成立，則有很多不可比較於aleph-1並大於aleph-0的其他基數。但是在任何情況下，沒有基數大於aleph-0並小於aleph-1。
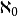
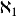
1）
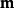是超限基數。就是說有一個戴德金無限集合
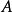使得
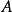的勢是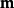
；
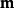
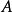
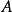
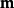
2）
；
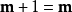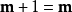
3）
；
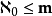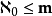
4）有一個基數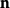
使得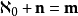
。
