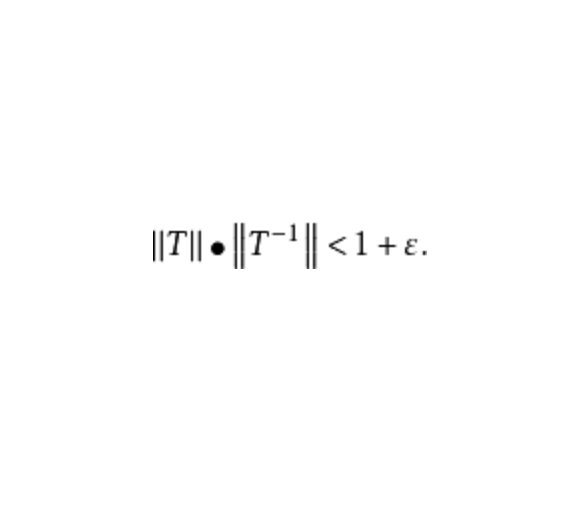基本介紹
- 中文名：超自反巴拿赫空間
- 外文名：super-reflexive Banach space
- 定義：一類自反空間
- 相關：巴拿赫空間、一致凸賦范線性空間
- 一級學科：數學
- 二級學科：泛函分析
定義,巴拿赫空間,一致凸賦范線性空間,
定義
超自反巴拿赫空間(super-reflexive Banach space)一類自反空間。巴拿赫空間X稱為超自反的，如果每個在X中有有限表示的巴拿赫空間Y都是自反的。一個賦范空間Y稱為在另一個賦范空間X中有有限表示是指：如果對Y的任何有限維子空間Yn和ε>0，存在X中有限維子空間Xn，及可逆的連續線性運算元T：Yn→Xn，使得
超自反空間一定是自反空間。兩個線性同胚的巴拿赫空間具有相同超自反性。超自反性和凸性的研究有密切的聯繫。例如，巴拿赫空間X超自反的一個充分必要條件為，在X上可賦予與原範數等價的一致凸範數。
巴拿赫空間
巴拿赫空間（Banach space）是指按範數導出的距離完備的賦范線性空間。設
為賦范線性空間，對
定義了X上的一個距離，使X成為度量空間。如果X按這個距離是完備的，就稱X為巴拿赫空間。
等都是巴拿赫空間的例子。
巴拿赫空間（含賦范空間）是1922年巴拿赫（Banach，S.）與維納（wiener，N.）相互獨立提出的，並且在不到10年的時間內便發展為相當完美而又有多方面套用的理論。1932年，巴拿赫論述這部分理論的《線性運算元理論》一書的問世，是泛函分析作為獨立的數學分支出現的標誌。巴拿赫空間至今仍是泛函分析研究的基本對象之一。
一致凸賦范線性空間
一致凸賦范線性空間（uniformly convex normed linear space）是滿足一致凸性的一類賦范線性空間。賦范線性空間稱為是一致凸的，如果對任意的 ε>0，存在 δ>0，使得當|| x ||≤1，|| y ||≤1並且|| x-y ||≥ε 時，必有 || x+y ||≥2-δ 成立。
是一致凸的。一致凸的巴拿赫空間是自反的。
一致凸空間是巴拿赫空間幾何理論的一個重要概念，它是克拉克松（Clarkson，J.A.）於1936年為研究拉東-科迪姆性質而引入的，他開創了從巴拿赫空間的幾何結構出發來研究巴拿赫空間性質的方法。巴拿赫空間的幾何學近年來一成為巴拿赫空間理論研究中人們特別感興趣的一個領域。
