質項

質項(prime)是特殊的小項，設R為真值函式f的卡諾圖的合塊，若f的其他任何合塊都不能覆蓋R，則R稱為f的質塊，質塊的對應小項稱為f的質項。質項有下列性質：1.若φ為f的最簡式，則φ必為f的某些質項之和；2.若f≠0，則f必有質項，而且只有有限個；3.f等於它的全部質項之和。因此，可以由質項求最簡式。

基本介紹

• 中文名：質項
• 外文名：prime
• 全稱：質蘊含項
• 簡介：質塊的對應小項

基本概念

質項：（1）在求蘊含項的過程中凡能不參加合併的項或合併後最終結果的項，稱為質蘊含項，簡稱質項。

（2）在“與-或”表達式中，如果一個“與”項不是其他“與”項的子集，則該“與”項稱為質項。例如，函式

中，不是質項，因為它是AC項的子集。從式(1)的卡諾圖(見圖1)上可以看出這一點：對應的卡諾圈含於AC對應的卡諾圈中；除外，其他“與”項都是質項，因為它們對應的卡諾圈不能被其他卡諾圈含入。

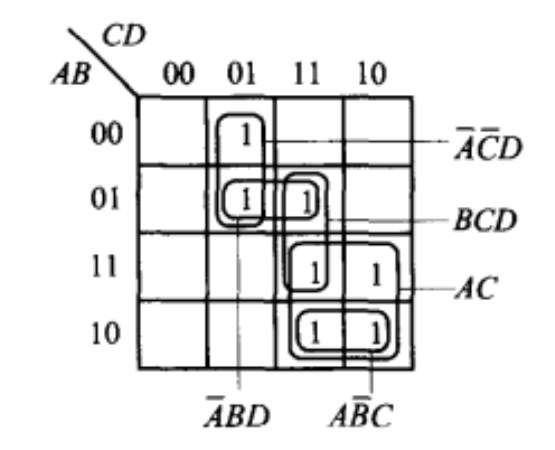
圖1

由圖1可見，函式中的非質項可以去掉，使函式得到化簡。但去掉全部非質項後的函式不一定為最簡。

必質項 必質項是“必要質蘊涵項”的簡稱。在“與-或”表達式中，如果一個質項含

有其他所有質項中都不曾包含的最小項，則該質項稱為必質項。顯然，式(1)中的AC和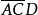是必質項。這在卡諾圖中反映的現象是，必質項卡諾圈中含有未被其他質項卡諾圈包圍的成分。 ·

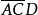
以上討論說明，在函式表達式中，非質項是可以去掉的項，必質項是不可去掉的項。但全部必質項之和不一定就是函式的最簡表達式。顯然，在圖1中，僅由必質項AC和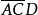不足以覆蓋全部為1的小方格，還必須再保留一個質項。

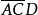
質項的性質

質項的性質：

(1)質項都是由1個、2個、2²個、2³個……最小項合併而成的。

(2)質項都是蘊含項。

乘積項P為F的質項的充分必要條件是：P的任何因式都不是F蘊含項。

從質項的產生過程可知：

(1)F的每一個蘊含項都以某個或某幾個質項為因子，因此全體質項可以把全體蘊含項吸收掉。

(2)F等於全體質項之和。

相關介紹

1.用列表化簡法化簡函式表達式的基本思路如下：

(1)用最小項表達式表示函式。

(2)求出函式的全部質項。

(3)從質項中提取全部必質項。

(4)如果全部必質項能覆蓋函式的全部最小項，則化簡完成。否則，應從剩下的質項中找出能覆蓋函式的最簡單的質項。

2.設邏輯函式F的全體質項為。令P_i對應一個邏輯變數，取值為0或1，i=1，2，…，n。若P_i在F的某一質項中出現(全體質項可以構成若干個質項和，最簡表達式就是一種或幾種質項和。P_i可在某一或某些質項和中出現，不在另一質項和中出現)，=1，P_i不在某一質項和中出現；=0則稱為P_i出現因子。