賈德克不等式

賈德克不等式是多項式導數的點態估計不等式，這個不等式是賈德克於1956年建立的。

基本介紹

• 中文名：賈德克不等式
• 外文名：Dzjadyk inequality
• 適用範圍：數理科學

簡介

賈德克不等式是多項式導數的點態估計不等式。

這個不等式是賈德克於1956年建立的，它在逼近論的逆定理研究中起著重要作用。

主要內容

設ω(t)是連續性模，即ω(t)是定義在[0,2]上有如下性質的函式：當t→0時，ω(t)→0。ω(t)≥0而且是t的增函式；對t₁,t₂∈[0,2](t₁+t₂≤2)，成立不等式ω(t₁+t₂)≤ω(t₁)+ω(t₂)。又設P_n(x)是次數不高於n的代數多項式，r是整數。如果在[-1,1]上有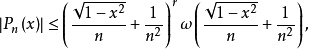

則在[-1,1]成立著

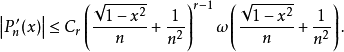這裡C_r是僅與r有關的正數。

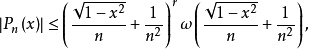
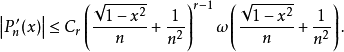
逼近論

逼近論是數學的一個分支，是研究用較簡單的函式，如多項式、三角多項式等來代替（逼近）較複雜的函式的理論。

逼近論的主要問題是：逼近函式的存在性，構造力一法，近似程度。與插值法聯繫密切。