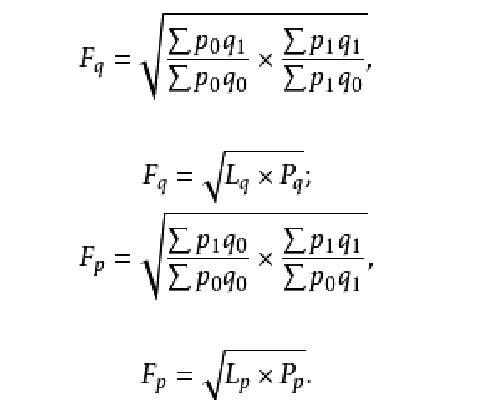費舍理想指數

Fisher理想指數(Fisher's ideal indices)也叫費希爾理想指數、費舍理想指數等，它包括價格指數和物量指數。費希爾理想價格指數是拉氏價格指數和帕氏價格指數的幾何平均值，即：F_p=(L_p·P_p)^1/2；費希爾理想物量指數是拉氏物量指數和帕氏物量指數的幾何平均值，即：F_q=(L_q·P_q)^1/2。費希爾將這兩個指數稱為“理想”指數是因為它們符合他認為重要的各種檢驗，例如“時間轉換”和“因子轉換”檢驗。時間轉換檢驗要求以時期0為基礎的時期t的指數應是以時期t為基礎的時期0的指數的倒數。因子轉換檢驗要求價格指數和物量指數的乘積應等於現值的對稱變化ΣV_t/ΣV₀。拉氏指數和帕氏指數本身通不過這兩種檢驗。因此，費希爾指數有很大的吸引力，在經濟統計中被廣泛使用。

基本介紹

• 中文名：費舍理想指數
• 外文名：Fisher's ideal indices
• 所屬學科：數學（統計學）
• 別名：Fisher理想指數、費希爾理想指數
• 提出者：統計學家Fisher
• 提出時間：1922
• 相關概念：拉氏指數、帕氏指數等
• 套用學科：經濟統計

基本介紹

理想指數(Idealindex)美國的統計學家Fisher(翻譯為費舍、費雪、費希爾、費休等)於1922年提出的，它是基期加權綜合指數(即拉氏指數) 與現期加權綜合指數(即帕氏指數)加以幾何平均得出的一種指數。有兩種形式：理想物量指數和理想價格指數，公式如下：

或 者

或者

和分別表示理想物量指數與理想價格指數，和分別表示拉氏物量指數與拉氏價格指數，和分別表示帕氏物量指數與帕氏價格指數。理想指數的優點在於它用幾何平均的方法，把拉氏指數和帕氏指數或者是把基期加權指數和現期加權指數所具有的相反方向的偏誤加以矯正，既糾正了用基期加權往往會使計算結果偏低，又糾正了用現期加權往往會使計算結果偏高的傾向，從而使其偏誤相互抵銷而得出比較準確、理想的指數。

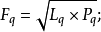
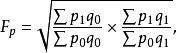
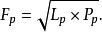
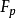
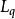
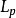
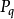
Fisher理想指數的優缺點

優點

Fisher理想指數有著許多令人滿意的統計和經濟理論上的性質，能夠滿足些重要的統計檢驗，如時間轉換檢驗和因子轉換檢驗等(而拉氏指數和派氏指數本身都不能通過這些檢驗)。同時由於Fisher理想指數體系融綜合指數的兩套分析體系於一體，兼顧並中和了拉氏指數和派氏指數由於權數選擇不同而導致的差異性，從而避免了綜合指數的失真性。正是由於Fisher指數所具有的良好性質，它在經濟統計中被廣泛套用，有著很大的吸引力。

缺點

儘管Fisher 指數是“理想的”，但它仍然存在一些不足之處：首先，Fisher指數要求它的數據達到能計算拉氏指數和派氏指數的要求，數據需求量大。這不僅會增加核算費用，而且會由於工作量的加大而導致計算和結果公布的延遲。其次，Fisher指數不像拉氏指數和派氏指數那樣容易理解。拉氏指數和派氏指數可以簡單地解釋為計量指定的一攬子貨物和服務的價值變化，而Fisher指數不可以。再次，Fisher指數不具有可加一致性，即使對於最基本的年度間數據變化也是如此。這一缺陷嚴重製約了它在核算框架中的套用。