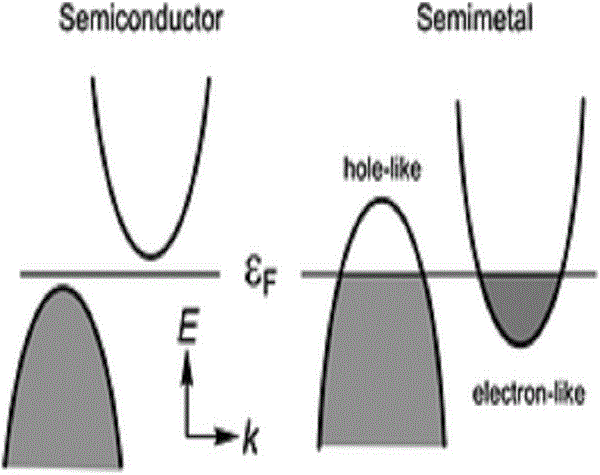
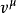基本介紹
- 中文名:費米-沃克移動
- 外文名:Fermi–Walker transport
- 學科:物理
數學表示,費米 - 沃克分化,共同移動坐標系,
數學表示
費米-沃克移動(Fermi-Walker transport)是廣義相對論中的一種移動。當某一曲線上的矢量場的弗米-沃克導數為零時,稱該矢量場沿該曲線作費米-沃克移動。在慣性參考系中,弗米-沃克導數與協變導數一致。
假設在曲線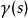 上有一矢量場X,則費米-沃克導數的定義為:
上有一矢量場X,則費米-沃克導數的定義為:
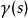
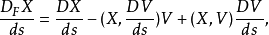
其中V為四維速度,D為黎曼空間中的協變導數。當
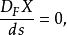
費米 - 沃克分化
在洛倫茲流形理論中,費米 - 沃克分化是協變分化的推廣。在廣義相對論中,相對於幀場中的時間單位矢量場而言,幀場中的類空矢量場的費米 - 沃克導數用於定義非慣性和非旋轉幀,通過規定費米 - 沃克衍生品應該消失。在慣性框架的特殊情況下,費米 - 沃克衍生物減少為協變導數。
隨著一個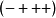 符號約定,這是沿著曲線為矢量場X定義的
符號約定,這是沿著曲線為矢量場X定義的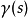 :
:
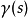
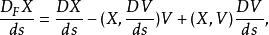
其中V是四速度,D是協變導數。如果
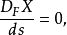
然後,矢量場X是沿曲線傳輸的費米 - 沃克(參見霍金和埃利斯,第80頁)。垂直於閔可夫斯基時空中四速度空間的向量,例如極化向量,在費米 - 沃克運輸下體驗托馬斯進動。
使用費米導數,Bargmann-Michel-Telegdi方程用於外部電磁場中的電子自旋進動可以寫成如下:
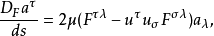
其中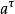 和
和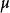 極化四矢量和磁矩,
極化四矢量和磁矩,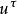 是四速電子,
是四速電子,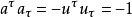 和
和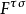 是電磁場強度張量。
是電磁場強度張量。
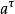
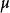
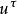
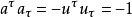
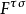
共同移動坐標系
可以定義與粒子共同移動的坐標系。如果我們採用單位向量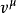 因為在共同移動坐標系中定義一個軸,那么任何用適當時間轉換的系統都被稱為正在進行費米沃克移動。
因為在共同移動坐標系中定義一個軸,那么任何用適當時間轉換的系統都被稱為正在進行費米沃克移動。