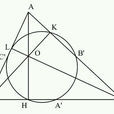
九點圓是幾何中一著名問題。據載在英國1804年的一種雜誌上,貝宛提出過這個問題。其實,歐拉在1756年就證明了“垂三角形和中位三角形有同一外接圓”,所以有時人們把這個定理歸功於歐拉,並稱該圓“歐拉圓”。九點圓的第一個完整的證明是龐斯萊在1821年發表的,所以應稱該圓為“龐斯萊圓”。1822年,費爾巴哈在他的論文裡也給出證明,還添進很多出人意料的性質,以致後人長把九點圓叫做“費爾巴哈圓”。
The Feuerbach Circle
三角形中三邊的三個中點、三個高的垂足和高的交點到各頂點的線段的三個中點在一個圓上.
推論1:三角形九點圓的半徑是該三角形外接圓半徑的一半。
推論2:一垂心組的四個三角形有一個公共的九點圓。
推論3:垂心組的四點為三角形頂點的四個三角形的外心另成一垂心組,且此垂心組各點與已知垂心組各點關於九點圓圓心對稱。