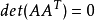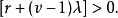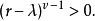基本介紹
- 中文名:費希爾不等式
- 外文名:Fisher's inequality
- 所屬學科:數學(組合學)
- 簡介:反映設計存在的一種條件
基本介紹,費希爾不等式的證明,
基本介紹
費希爾不等式在(b,v,r,k,λ)設計中,b≥v。
雷·喬德里(D.K.Ray-Chaudhuri)和威爾森(R.M.Wilson)將這個不等式推廣到t設計的情形。他們證明:若2s-(v,k,λ)設計存在,且v≥k+s,則

若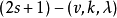 設計存在,且
設計存在,且 ,則
,則
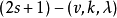


費希爾不等式的證明
為了證明這一結果,需要引入一個很有幫助的概念,這就是區組設計的關聯矩陣(incidence matrix),如果一個設計有變元 ,區組
,區組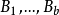 ,那么A是一個由0和1組成的v×b矩陣,其中,如果xi在Bj中則A的i,j項是1,否則它是0(這就是點集關聯矩陣)。
,那么A是一個由0和1組成的v×b矩陣,其中,如果xi在Bj中則A的i,j項是1,否則它是0(這就是點集關聯矩陣)。

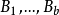
為了證明費希爾不等式,我們先給出以下結果,其證明請參考相應文獻。
定理1 在一個(b,v, r, k,λ)設計中有
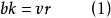
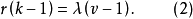
定理2如果A是(b,v, r, k,λ)設計的關聯矩陣,那么

費希爾不等式的證明:
我們假設b<v,並推導出一個矛盾。設A是關聯矩陣。
因為b<v,所以我們可以把v-b個0列加到A上,結果給出一個v×v方陣B,現在AAT= BBT,因為A的兩行的內積等於B的兩行的內積。取行列式,我們得出下面的結論:
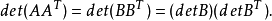
但是,detB=0,因為B有0列。因此,det(AAT)=0。現在,根據定理2,有



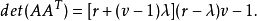
因為我們已得出結論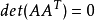 ,所以我們有
,所以我們有