貝爾曼一格朗沃爾不等式

在數學中，格朗沃爾不等式（也稱為格朗沃爾引理或貝爾曼一格朗沃爾不等式）允許通過相應的微分或積分方程的解來將一個已知的函式約束為滿足一定的微分或積分不等式的函式。有兩種形式的引理，差分形式和整體形式。後者有幾種變體形式。

格朗沃爾不等式是在普通和隨機微分方程理論中獲得各種估計的重要工具。特別地，它提供了可以用於證明解初始值問題的唯一性的比較定理。

它的命名來自Thomas HakonGrönwall（1877-1932）。 格朗沃爾是他的名字的瑞典語拼寫，但是在移民到美國後，他將他的名字命名為格朗沃爾在他的科學出版物中。

差分形式由格朗沃爾在1919年證明。整體形式由理察貝爾曼於1943年證明。

貝爾曼一格朗沃爾不等式的非線性泛化被稱為Bihari-LaSalle不等式。

基本介紹

• 中文名：貝爾曼一格朗沃爾不等式
• 外文名：Bellman-Gronwall inequality
• 領域：數學
• 形式：差分形式、整體形式
• 證明人：貝爾曼和格朗貝爾
• 得證時間：1919年和1943年

格朗沃爾簡介

Thomas HakonGrönwall或Thomas Hakon Gronwall（1877年1月16日，瑞典Dylta bruk-1932年5月9日，紐約市）是瑞典數學家。 他在斯德哥爾摩大學和烏普薩拉大學學習，並完成了他的博士學位。 在1908年，在烏普薩拉州，Grönwall在德國移民到美國之前，曾在德國工作了大約一年的時間。他後來在普林斯頓大學攻讀數學，從1925年開始，他是哥倫比亞大學物理系的成員。

1925年，他開始與維克多·拉默（Victor LaMer）合作，導致他於1927年加入哥倫比亞大學物理系，擔任助理。這是一個很好的機會。 由於沒有教學義務，他完全控制了自己的時間和豐富的新的有趣的問題，以解決物理化學和原子物理學問題。 他在Debye-Hückel理論中開發出了更高近似度的解決方案。

貝爾曼簡介

貝爾曼於1920年出生於紐約市，擁有波蘭和俄羅斯血統，他的猶太人父母是珍珠（néeSaffian）和約翰·詹姆斯·貝爾曼（John James Bellman），他們在布魯克林卑爾根街附近的Prospect Park營了一家小雜貨店。他於1937年出生於布魯克林的亞伯拉罕·林肯高中，並在布魯克林學院學習數學，1941年獲得了學士學位，後來獲得威斯康星大學麥迪遜分校的碩士學位。在二戰期間，他曾在洛斯阿拉莫斯的理論物理司組工作。在1946年，他在普林斯頓大學獲得博士學位，在所羅門·萊夫謝茨的監督之下。從1949年開始，Bellman在蘭德公司工作多年，在此期間他開發了動態規劃。

後來在生活中，理察·貝爾曼的興趣開始強調生物學和醫學，他被認為是“當代科學的前沿”。 1967年，他成為“數學生物科學”雜誌的創始編輯，專門出版醫學和生物學專題的套用數學研究。 1985年，貝爾曼數學生物科學獎是以他的榮譽創立的，每兩年向該雜誌的最佳研究論文頒獎。

貝爾曼於1973年被診斷患有腦腫瘤，已被除去，但導致併發症，使他嚴重殘疾。他是南加州大學教授，美國藝術與科學學院研究員（1975年），國家工程院院士（1977），和國家科學院院士的科學（1983）。

他於1979年獲得IEEE榮譽勳章，“對決策過程和控制系統理論的貢獻，特別是動態規劃的創造和套用”。他的關鍵工作是貝爾曼方程式。

數學辭海中的定義

貝爾曼一格朗沃爾不等式(Bellman-Gronwall inequality)用於估計線性積分不等式解的一個不等式。設函式y(t)滿足積分不等式：

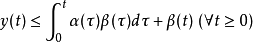
式中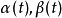是已知實函式，則下列貝爾曼一格朗沃爾不等式：

對成立。如果是可微的，則有：

特別地，當a<t}恆為常數時，則有：

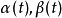
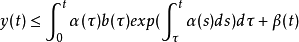
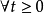
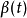
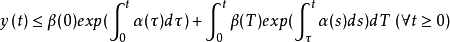
差分形式

用I和a<b表示形式為[a,∞)或[a,b]或[a,b)的實線區間。用β和μ表示在區域I上的連續實數函式。如果μ在I內是可微的並且滿足以下差分不等式：

那么μ定與差分方程的解有如下關係：

對所有t∈I都成立。

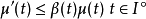
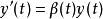
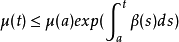
證明：定義函式v(t)為：

並且v滿足：

並對所有的t∈I都有：v(a)=1和v(t)>0，那么有：

那么函式的導數是非正的並且函式的值必定大於它在區間I起始點a的函式值：

上述即為格朗貝爾不等式。證明完畢。

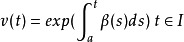
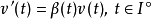
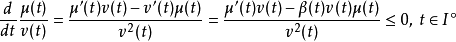
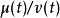
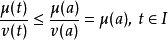
對連續函式的整體形式

用I和a<b表示形式為[a,∞)或[a,b]或[a,b)的實線區間。用β和μ表示在區域I上的連續實數函式。假設β和μ是α在區間I上的連續、函式值為負的部分。那么：

a)如果β是非負的並且μ滿足整體不等式：

那么：

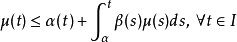
b)另外，如果函式α是非遞減函式，那么：

備註：對於函式α和u的符號沒有假設；與微分形式相比，積分形式不需要u的微分性。