方法概述 當前,從研究範式的特徵和視角來劃分,股票投資分析方法主要有如下三種:
基本分析 、
技術分析 、
演化分析 。這三種分析方法所依賴的理論基礎、前提假設、研究範式、套用範圍各不相同,在實際套用中它們既相互聯繫,又有重要區別。其中基本分析屬於一般經濟學範式,技術分析屬於數理或牛頓範式,演化分析屬於生物學或達爾文範式;基本分析主要套用於投資標的物的選擇上,技術分析和演化分析則主要套用於具體操作的時機和空間判斷上,作為提高股票投資分析有效性和可靠性的重要手段。
在評估股市波動風險與投資機會的方法中,貝塔係數是衡量結構性與系統性風險的重要參考指標之一,其真實含義就是個別資產及其組合(個股波動),相對於整體資產(大盤波動)的偏離程度。
基本定義 貝塔係數是
統計學 上的概念,它所反映的是某一投資對象相對於大盤的表現情況。其絕對值越大,顯示其收益變化幅度相對於大盤的變化幅度越大;絕對值越小,顯示其變化幅度相對於大盤越小。如果是負值,則顯示其變化的方向與大盤的變化方向相反;大盤漲的時候它跌,大盤跌的時候它漲。由於我們投資於投資基金是為了取得專家理財的服務,以取得優於被動投資於大盤的表現情況,這一指標可以作為考察基金經理降低投資波動性風險的能力。在計算貝塔係數時,除了基金的表現數據外,還需要有作為反映大盤表現的指標。根據投資理論,全體市場本身的β係數為1,若基金投資組合淨值的波動大於全體市場的波動幅度,則β係數大於1。反之,若基金投資組合淨值的波動小於全體市場的波動幅度,則β係數就小於1。β係數越大之證券,通常是投機性較強的證券。以美國為例,通常以標準普爾五百企業指數(S&P 500)代表股市,貝塔係數為1。一個共同基金的貝塔係數如果是1.10,表示其波動是股市的1.10 倍,亦即上漲時比市場表現優10%,而下跌時則更差10%;若貝塔係數為0.5,則波動情況只及一半。β= 0.5 為低風險股票,β= 1.0 表示為平均風險股票,而β= 2.0 → 高風險股票,大多數股票的β係數介於0.5到1.5間 。
β係數 貝塔係數衡量股票收益相對於業績評價基準收益的總體
波動性 ,是一個相對指標。 β 越高,意味著股票相對於業績評價基準的波動性越大。 β 大於 1 ,則股票的波動性大於業績評價基準的波動性。反之亦然。
如果 β 為 1 ,則市場上漲 10 %,股票上漲 10 %;市場下滑 10 %,股票相應下滑 10 %。如果 β 為 1.1, 市場上漲 10 %時,股票上漲 11%, ;市場下滑 10 %時,股票下滑 11% 。如果 β 為 0.9, 市場上漲 10 %時,股票上漲 9% ;市場下滑 10 %時,股票下滑 9% 。
Beta係數起源於資本資產定價模型(CAPM模型),它的真實含義就是特定資產(或資產組合)的系統風險度量。
所謂
系統風險 ,是指資產受巨觀經濟、市場情緒等整體性因素影響而發生的價格波動,換句話說,就是股票與大盤之間的聯動性,系統風險比例越高,聯動性越強。
β係數的取法 與系統風險相對的就是個別風險,即由公司自身因素所導致的價格波動。
總風險=系統風險+個別風險
而Beta則體現了特定資產的價格對整體經濟波動的敏感性,即,市場組合價值變動1個百分點,該資產的價值變動了幾個百分點——或者用更通俗的說法:大盤上漲1個百分點,該股票的價格變動了幾個百分點。
用公式表示就是:
實際中,一般用單個股票資產的歷史收益率對同期指數(大盤)收益率進行回歸,回歸係數就是Beta係數。
計算方式 單項資產 (註:槓桿主要用於計量非系統性風險)
β係數 單項資產系統風險用β係數來計量,通過以整個市場作為參照物,用單項資產的風險收益率與整個市場的平均風險收益率作比較,即:
其中Cov(ra,rm)是證券 a 的收益與市場收益的協方差;
β計算公式 是市場收益的方差。
因為:Cov(r a ,r m ) = ρa m σa σm
所以公式也可以寫成:
其中ρ
a m 為證券
a 與市場的相關係數;σ
a 為證券
a 的標準差;σ
m 為市場的標準差。
β計算公式 據此公式,貝塔係數並不代表證券價格波動與總體市場波動的直接聯繫。
不能絕對地說,β越大,證券價格波動(σa )相對於總體市場波動(σm )越大;同樣,β越小,也不完全代表σa 相對於σm 越小。
甚至即使β = 0也不能代表證券無風險,而有可能是證券價格波動與市場價格波動無關(ρa m = 0),但是可以確定,如果證券無風險(σa ),β一定為零。
注意:掌握β值的含義
◆ β=1,表示該單項資產的風險收益率與市場組合平均風險收益率呈同比例變化,其風險情況與市場投資組合的風險情況一致;
◆ β>1,說明該單項資產的風險收益率高於市場組合平均風險收益率,則該單項資產的風險大於整個市場投資組合的風險;
◆ β<1,說明該單項資產的風險收益率小於市場組合平均風險收益率,則該單項資產的風險程度小於整個市場投資組合的風險。
小結:1)β值是衡量系統性風險,2)β係數計算的兩種方式。
貝塔係數 公式為:
其中Cov(ra,rm)是證券 a 的收益與市場收益的協
方差 ;是市場收益的方差。
因為:
Cov(ra,rm) = ρamσaσm
所以公式也可以寫成:
其中ρam為證券 a 與市場的相關係數;σa為證券 a 的標準差;σm為市場的標準差。
貝塔係數利用回歸的方法計算: 貝塔係數等於1即證券的價格與市場一同變動。
貝塔係數高於1即證券價格比總體市場更波動。
貝塔係數低於1即證券價格的波動性比市場為低。
如果β = 0表示沒有風險,β = 0.5表示其風險僅為市場的一半,β = 1表示風險與市場風險相同,β = 2表示其風險是市場的2倍。
一般用途 一般的說,Beta的用途有以下幾個:
1)計算
資本成本 ,做出投資決策(只有
回報率 高於資本成本的項目才應投資);
2)計算資本成本,制定業績考核及激勵標準;
3)計算資本成本,進行資產估值(Beta是
現金流貼現 模型的基礎);
4)確定單個資產或組合的
系統風險 ,用於
資產組合 的投資管理,特別是股指期貨或其他金融衍生品的避險(或投機)。
對Beta第四種用途的討論將是本文的重點。
投資組合的β係數 組合Beta
Beta
係數 有一個非常好的線性性質,即,資產組合的Beta就等於單個資產的Beta係數按其在組合中的權重進行加權求和的結果。
5) 貝塔係數在證券市場上的套用
貝塔係數反映了
個股 對市場(或
大盤 )變化的敏感性,也就是個股與大盤的相關性或通俗說的“
股性 ”。可根據市場走勢預測選擇不同的貝塔係數的證券從而獲得額 外收益,特別適合作
波段操作 使用。當有很大把握預測到一個大
牛市 或大盤某個不漲階段的到來時,應該選擇那些高貝塔
係數 的證券,它將成倍地放大市場
收益率 ,為你帶來高額的收益;相反在一個熊市到來或大盤某個下跌階段到來時,你應該調整
投資結構 以抵禦
市場風險 ,避免損失,辦法是選擇那些低貝塔係數的證券。
為避免
非系統風險 ,可以在相應的市場走勢下選擇那些相同或相近貝塔係數的證券進行
投資組合 。比如:一支
個股 貝塔係數為1.3,說明當
大盤 漲1%時,它可能漲1.3%,反之亦然;但如果一支個股貝塔係數為-1.3時,說明當大盤漲1%時,它可能跌1.3%,同理,大盤如果跌1%,它有可能漲1.3%。
影響因素 β
係數 是度量某種(類)
資產價格 的變動受市場上所有資產價格平均變動影響程度的指標,是採用收益法評估企業價值時的一個關鍵的企業
系統風險 係數。評估人員有必要對影響β係數的各種因素進行分析,以恰當確定評估對象的系統風險。
涉及β係數
確定β係數的模型有兩種形式。一種是CAPM模型(資本資產定價模型,也稱證券市場線模型,security market line):E(Ri)= Rf+βi(Rm-Rf) 其中:E(Ri)= 資產i的期望收益率
另一種是市場模型:E(Ri)=αi+βiRm
這兩個模型都是單變數線性模型,都可用最小二乘法確定模型中的參數。在這兩個模型中,β
係數 都是模型的斜率。當αi = Rf(1-βi)時,這兩個模型是可以互相轉換的。
但是,這兩個模型的假設前提、變數所採用的數據和套用條件都不相同。從理論上說, CAPM模型是建立在一系列嚴格的假設前提下的均衡模型。其假設前提是完備的市場、信息無成本、資產可分割、投資者厭惡風險、投資者對收益具有共同期望、投資者按無風險
資產收益率 自由借貸等。即CAPM模型是描述市場處於均衡狀態下的資產
期望收益率 E(Ri)與
資產風險 補償(Rm-Rf)的關係。而市場模型是描述資產期望收益率與市場
平均收益率 之間的關係。市場模型體現的是資產的期望收益率與市場期望收益率之間的關係,而不論該市場是否處於均衡狀態。其中的β
係數 體現的是市場的期望收益率變動對資產期望收益率變動影響的程度。
採用CAPM模型確定β係數,必然要涉及
無風險收益率 ,從而引起了對該模型的爭議。
布萊克 (Black,1972)在《限制借貸條件下的資本市場均衡》一文中指出:由於通貨膨脹的存在,真正的
無風險利率 是不存在的。因此布萊克認為,CAPM模型的基礎本身就存在問題。但CAPM模型還是普遍地得到了套用。在美國,CAPM模型中的無風險收益率採用的是長期
國債利率 。
證券對β係數的影響
以下分別以寶鋼股份(600019)與桂林旅遊(000978)兩隻股票來說明不同市場指數條件對β
係數 確定的影響。首先以寶鋼股份2005年4月29日至2007年6月30日的股票月底
收盤價 的變動情況分別對上證
綜合指數 、滬深300對應的月底收盤價的變動情況進行回歸,得出寶鋼股份在這段時間兩種指數情況下的β係數:
分別採用兩種指數回歸得出β係數分別為0.9789和0.9439,還比較接近。
下面是以桂林旅遊2005年4月29日至2007年12月28日的股票月底收盤價的變動情況分別對上證綜合指數、滬深300、深證
成分指數 、
深證綜合指數 對應的月底收盤價的變動情況進行回歸。
根據得出的回歸方程可知(以深證成份指數和深證綜合指數的
變動率 為市場
收益率 的回歸分析圖與回歸方程略),以上證綜合指數、滬深300指數、深證成份指數和深證綜合指數的變動率作為市場收益率時,桂林旅遊的β
係數 分別為0.7466、0.7511、0.6259和0.7988。
桂林旅遊是深市上市的股票,不包含在上證
綜合指數 、滬深300指數和深證成份指數的樣本中,僅是深證綜合指數中的樣本。在深證綜合指數的變動率作為市場收益率時的β係數深證成份指數的變動率作為市場收益率時的β係數相差了17.29個百分點。所以說,在選用不同的證券指數的
收益率 代表市場收益率時,將會對所計算出來的β係數有很大影響。
計算中影響
收益法 中的β係數應該是能代表未來的β係數。但我們計算β係數通常只能利用歷史數據,但所採用歷史數據的時段是長一些還是短一些好呢?採用數據的時段越長,β係數的
方差 將能得到改善,其穩定性可能會提高,但時段過長,由於企業經營的變化、市場的變化、技術的更新、競爭力的變遷、企業間的兼併與收購行為以及證券市場特徵的變化等都有可能影響β係數的計算結果。一般認為,
最佳的計算時段為4-6年 。下面以上證
綜合指數 的收益率作為市場
平均收益率 ,得出桂林旅遊在不同時段下的β
係數 如下:
可見,桂林旅遊β係數計算的時段不同,差異很大。
計算時段的影響
證券收益率 的單位時段可以按日、按周、按月計算。計算單位時段長短不同,可能會對β係數產生影響。對2002年至2007年期間的桂林旅遊和上證綜合指數分別按周和按月進行
收益率 計算,得出桂林旅遊在收益率不同單位時段情形下的不同的β係數。
按周計算收益率較按月計算收益率得出的β係數小。國外大多數的研究人員認為β係數計算應該採用月收益率。如果採用日收益率,雖然會增多許多觀察值,但會引起諸如非同步交易等問題。哈瓦威尼、科拉多和沙茨
伯格 (Hawawini,Corrado an Schatzberg,1991)的研究指出:如果使用日收益率資料計算β,由於收益率分布相對於常態分配呈寬尾狀,最小二乘法估計法可能無效。我國學者
吳世農 檢驗了1992年6月-1994年12月間在上海、深圳兩個
交易所 的20種
股票交易 日收益的統計分布,結果表明上交所的12種股票日
收益率 的頻率分布都明顯地不屬於常態分配,但深交所的8種股票中有6種股票日收益率的頻率分布近似於常態分配。徐迪和吳世農(2001)套用
赫斯特指數 檢驗,結果表明當前中國證券市場的日收益率趨於非常態分配。因此,收益率的單位計算時段的不同將可能導致收益率的頻率分布不同,從而使因β
係數 計算結果也不相同。
紅利發放對β係數的影響
由於β係數是根據市場
平均收益率 的變動情況與某種資產的收益率變動情況之間的關係確定的,所以,在計算β係數的時段內,當作為市場平均收益率的證券指數的樣本中發放紅利的證券所占比例較大時,則發放紅利的資產的β係數的計算結果受紅利發放的影響則比較小;反之,對於長期不發放紅利的資產證券,所受影響會很大。
其他可能影響β係數
我國學者吳世農等研究了1996年-2001年我國上市公司的公司規模、財務槓桿、經營槓桿、股利支付率、盈利變動性、流動比率、總資產增長率、主營收入增長率、主營業務利潤率、資本收益率、資本收益增長率等11個會計變數與β係數之間的相關關係。得出的結論是,β係數總體上與這些會計變數之間相關程度不高,相關檢驗的顯著性不強。
此外,巨觀經濟因素如經濟周期、利率、
通貨膨脹率 等對β
係數 的影響,尚需深入研究。
 β係數
β係數 β係數的取法
β係數的取法 β係數
β係數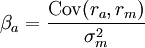 β計算公式
β計算公式
 β計算公式
β計算公式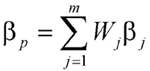 投資組合的β係數
投資組合的β係數
