變態圓(Abnormal circle)是一種特殊的圓,指半徑為零和無限長的圓,將點和直線分別看做半徑為零及半徑為無限長的圓,這兩種圓稱為變態圓。點作為變態圓時又稱為點圓。
基本介紹
- 中文名:變態圓
- 外文名:Abnormal circle
- 所屬學科:數學
- 所屬問題:平面幾何(圓)
變態圓方程











相關定理








變態圓的射影定義






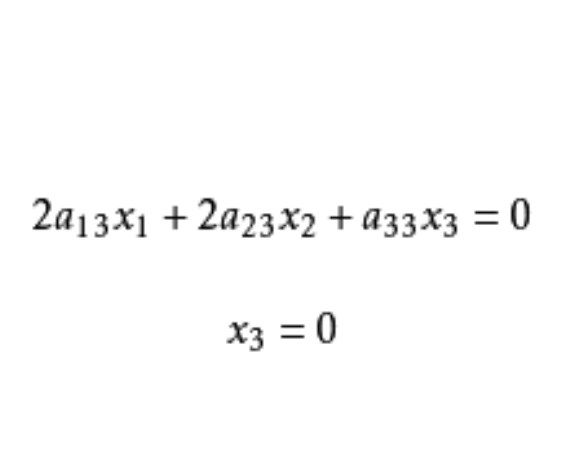
變態圓(Abnormal circle)是一種特殊的圓,指半徑為零和無限長的圓,將點和直線分別看做半徑為零及半徑為無限長的圓,這兩種圓稱為變態圓。點作為變態圓時又稱為點圓。

























變態圓(Abnormal circle)是一種特殊的圓,指半徑為零和無限長的圓,將點和直線分別看做半徑為零及半徑為無限長的圓,這兩種圓稱為變態圓。點作為變態圓時又稱為點圓。變態圓方程以 表示笛卡爾直角坐標,那么圓的方程可...
變態,指在有些生物的個體發育中,其形態和構造上經歷階段性劇烈變化。有些器官退化消失,有些器官有變化、得到改造,有新的性狀發生出來。主要由自身基因與外環境控制,這種現象統稱為變態。 如昆蟲結束幼蟲期進入成蟲期,建成成體結構;植物...
變態行為亦稱“實驗性神經症”。動物因病理條件而產生的行為。常與實驗引起的焦慮相聯繫。巴甫洛夫發現,在條件作用實驗時,動物的正常行為會突然崩潰,變得焦慮不安。如某實驗中讓一隻狗分辨橢圓形和圓形。圓形用食物強化,橢圓形不強化。
變態反應性皮膚病是指變態反應所致的炎症性皮膚病,又稱過敏性皮膚病,是較常見的一類皮膚病,其共同特點是均與過敏反應有關、有不同程度的瘙癢、抗過敏藥物治療有效、去除致敏因素方可治癒,常見的疾病有變態反應性接觸性皮炎、蕁...
變態莖(modification of stem) 由於功能改變引起的形態和結構都發生變化的莖。植物在長期系統發育的過程中,由於環境的變遷,引起器官形成某些特殊的適應,以致形態、結構都發生了改變的莖。莖的變態,有兩種發展趨向。變態部分,有的特別...
[13]螳螂屬於漸變態昆蟲。若蟲經8~9齡發育為成蟲,通常一年完成一個世代,以卵越冬,卵鞘附著於樹枝、竹枝、草莖、石塊等物體上,不同種的螳螂對附著的物體具有選擇性。若蟲成活率低,且有自殘現象;成蟲也具有自殘行為,尤其是在交配的過...
圓修律,動漫《R-15》中的角色。動漫人物 圓修 律(円修 律(えんしゅう りつ))聲優:村上圓香 角色簡介 和丈途關係十分好的男生,喜歡丈途。是個數學天才,在介紹時被霧線蘭說成「在大學的研究室與他人共同進行研究。卻...
