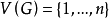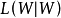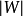基本介紹
- 中文名:變元矩陣-樹定理
- 外文名:variable matrix-tree theorem
- 所屬學科:數學
- 所屬問題:組合學(圖與超圖)
- 簡介:矩陣-樹定理的推廣
基本介紹,矩陣-樹定理,
基本介紹
若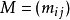 為對應於圖G的形式矩陣,其元素定義為:
為對應於圖G的形式矩陣,其元素定義為:
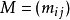
對於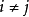 ,當
,當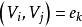 ,
, ;
;
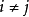
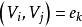

當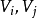 不相鄰,
不相鄰,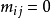 ,
,
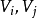
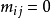
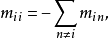
則M的任何代數餘子式的值是G的樹多項式,這稱為變元矩陣-樹定理。附圖為一示例。其中,P(T(G))為圈G的樹多項式。
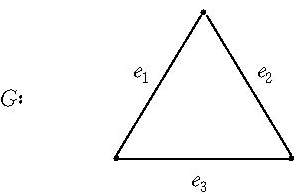 圖1
圖1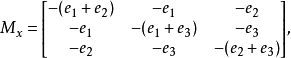
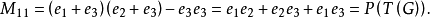
矩陣-樹定理
矩陣-樹定理 設G為一個具有頂點集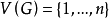 的圖。那么L(G)中任意元素的餘子式等於G中支撐樹的數量。
的圖。那么L(G)中任意元素的餘子式等於G中支撐樹的數量。
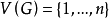
證明 在下文定理1中令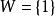 ,則
,則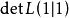 等於只有一個分支的G的支撐森林的數量,也就是等於G中支撐樹的數量。通過下文引理1可知,L(G)的所有餘子式是相等的,定理得證。
等於只有一個分支的G的支撐森林的數量,也就是等於G中支撐樹的數量。通過下文引理1可知,L(G)的所有餘子式是相等的,定理得證。
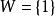
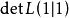
需要指出,在此定理中G並不需要被假設為連通圖。如果G是非連通的,則其沒有支撐樹。同時,L(G)的秩最多為n-2,因此其所有的餘子式都為0。
引理1 設G為一個具有頂點集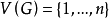 和邊集
和邊集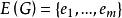 ,那么下述命題成立:
,那么下述命題成立:
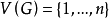
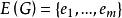
(i)L(G)為對稱的半正定矩陣。
(ii)L(G)的秩為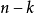 ,其中k為G中連通分支的數量。
,其中k為G中連通分支的數量。
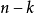
(iii)對於任意的向量x,有
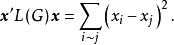
(iv)L(G)的每行元素與每列元素之和都為0。
(v)L(G)中任何兩個元素的餘子式相等。
定理1 設G為一個具有頂點集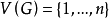 的圖,並令W為V(G)的一個非空真子集。那么
的圖,並令W為V(G)的一個非空真子集。那么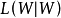 的行列式等於G中含有
的行列式等於G中含有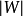 個分支的支撐森林的數量,其中每一個分支都包含了W中的一個頂點。
個分支的支撐森林的數量,其中每一個分支都包含了W中的一個頂點。