誘導速度

誘導速度是直升機(旋翼)空氣動力學裡一個重要的術語。所謂誘導速度，就是由於某種作用在均勻流場內或靜止空氣中所引起的速度增量(包括大小和方向的改變) 。

基本介紹

• 中文名：誘導速度
• 外文名：induced velocity
• 一級學科：航空宇航科學與技術
• 二級學科：飛行器設計
• 套用領域：直升機空氣動力學
• 相關理論：動量理論

概論

誘導速度是指空氣在流過某一物體後產生額外的速度，比如空氣在經過物體前速度為V0，經過該物體後速度變為V1，那么vi=V1-V0即為誘導速度。

對於我們直升機而言，旋翼與空氣相互作用，空氣因受旋翼作用而加速向下流動，空氣速度增加量就是該處的誘導速度值，同時空氣給旋翼與反作用力，即旋翼產生的拉力。直升機懸停時，由於空氣（槳盤上方無窮遠處）原來沒有速度，那么在槳盤下方的氣流速度就是誘導速度。

誘導速度與旋翼拉力，需用功率，飛行狀態關係密切。一般簡化計算均假設誘導速度均勻分布，而實際上誘導速度在空間不同位置是變化的。因此精確計算必須對誘導速度大小，分布規律的研究計算。

垂直飛行時

直升機在作垂直上升飛行時，0-0截面位於滑流區上游無窮遠處，該截面處氣流速度為直升機垂直上升速度 。而在1-1截面處，氣流經過槳盤後獲得了一個增量 ，速度變為 ，並且。氣流流動至下游很遠處的2-2截面後，速度則變為 。這裡， 為槳盤處的誘導速度， 為下游很遠處的誘導速度。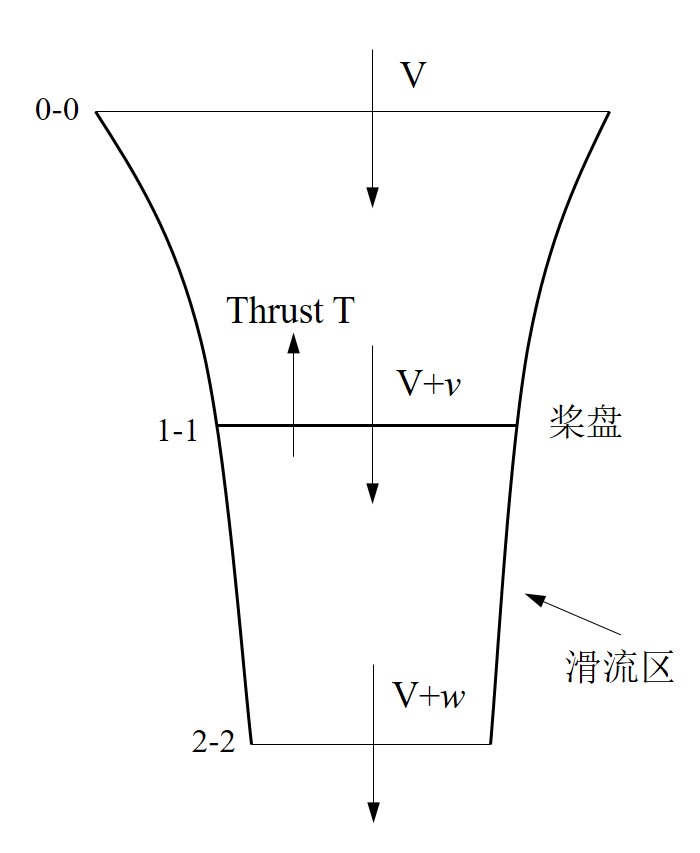

垂直上升時誘導速度示意圖

對旋翼滑流套用定常條件下的動量定理，不計空氣重量，設槳盤對氣流的作用力為 。假設氣流是無粘的，因此，滑流邊界上無切向力，僅受法向壓力。滑流是軸對稱的，其整個側面上壓強的水平橫向分量自相平衡，而軸向分量構成的總壓力與滑流上游0-0和下游2-2截面所受的總壓力互相平衡。因而，滑流所受外力合力為 ，而軸向速度由 增加至 ，再繼續變為 ，根據動量定理，可得： ，式中 為單位時間內流過滑流任一截面的空氣品質。那么，旋翼的拉力為 ，拉力的方向與滑流增速方向相反。

其次，對旋翼滑流套用定常條件下的能量守恆定律，仍不計重力。因為滑流上游處截面0-0與下游處截面2-2壓力所做的功率互相抵消，而側壁壓強與流速垂直，功率為0。所以，滑流的動能變化所需能量完全來自旋翼。那么，旋翼所消耗功率就可由滑流的動能變化率確定：

旋翼付出的功率則應為：

從式中可以看出，旋翼功率等於旋翼拉力與槳盤處氣流速度的乘積。在滑流理論中，該功率還可分為兩部分：一部分是拉力與運動速度 的乘積，稱為“有效功率”；另一部分是拉力與槳盤處誘導速度 的乘積，稱為“誘導功率”，純為損失。

聯立以上三式，可得

或

槳盤處的氣流速度，等於槳盤上游與下游處氣流速度之和的一半。也可表示為槳盤處的誘導速度，等於槳盤下游處誘導速度的一半。

而對於直升機垂直下降的狀態，其氣流速度方向發生了變化，並且在槳盤上游很遠處出現誘導速度，而槳盤下游很遠處的氣流速度則為垂直下降的速度。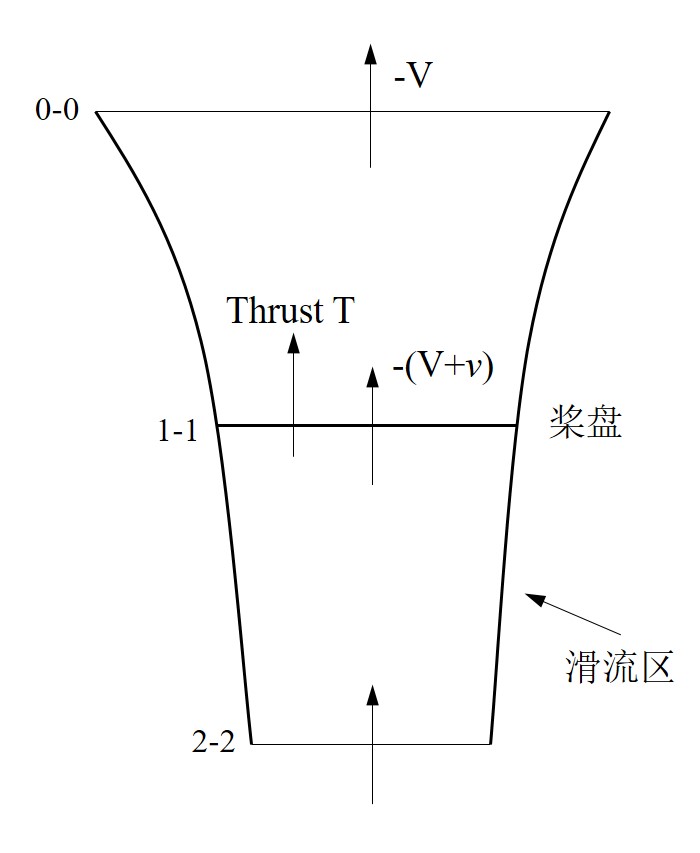

垂直下降時誘導速度示意圖

前飛時

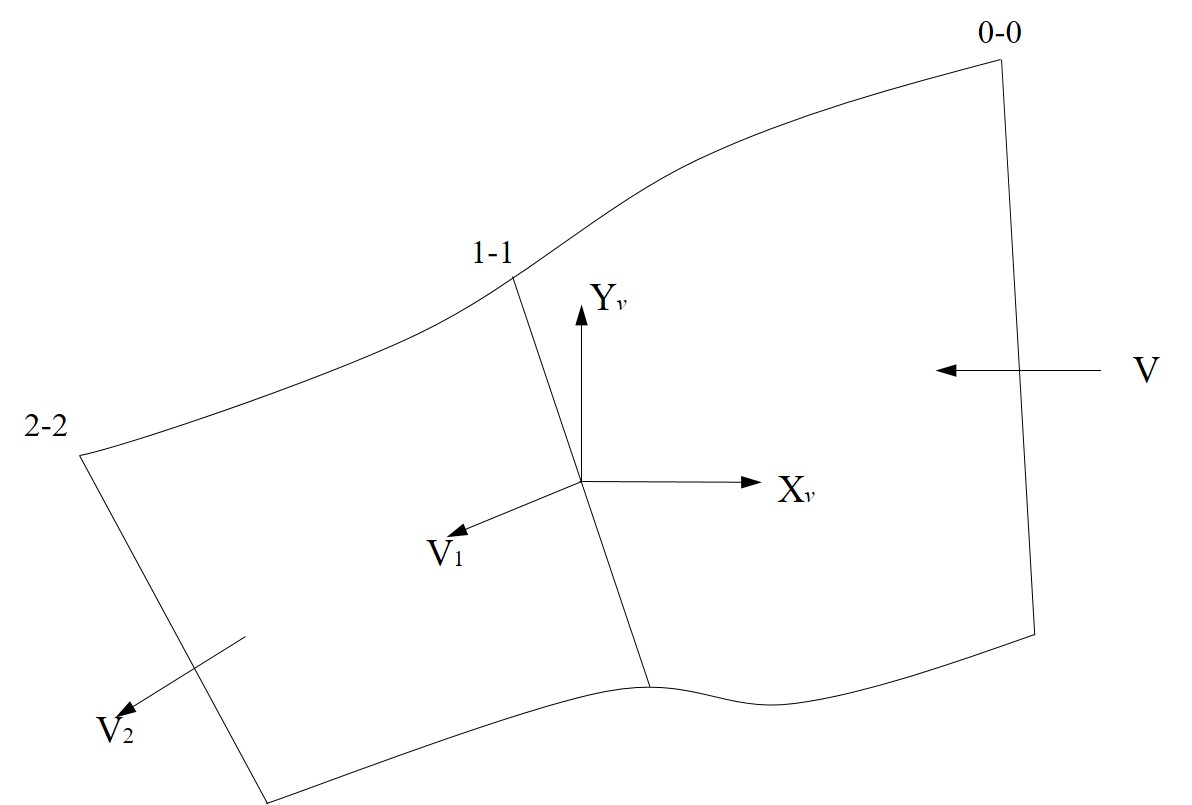前飛時誘導速度示意圖

直升機前飛時，處於斜流狀態，未擾動氣流經過槳盤後，不僅氣流速度大小改變，而且氣流速度方向也有偏轉，因此，任一截面處的氣流速度都是未擾動氣流速度與誘導速度的矢量和。將氣流速度與氣動力分解至速度坐標系。

上游0-0截面處氣流速度： ， ；誘導速度： ， 。

槳盤1-1截面處氣流速度： ， ；誘導速度： ， 。

下游2-2截面處氣流速度 ， ；誘導速度： ， 。

由動量定理有

式中 為空氣品質流量，各截面處的 均相等。

再根據動能定理，可得沿 和 方向的功率為

聯立以上各式可得

式中和分別為旋翼向前的推力和旋翼升力。

於是，可得

那么槳盤處誘導速度

由此可得出結論：在斜流狀態，旋翼槳盤處的誘導速度在數值上等於下游很遠處的誘導速度的一半，在方向上兩者彼此平行。