誘導比例

誘導比例(induced proportion)是比例的一種恆等變形，對於一個已知比例的某些項，施行某些運算，可以得到一些新的比例，這些新的比例叫做從已知比例得到的誘導比例。例如：合比定理、分比定理、合分比定理、等比定理、連比定理等，都是誘導比例。

基本介紹

• 中文名：誘導比例
• 外文名：induced proportion
• 所屬學科：數學
• 所屬問題：算術
• 簡介：比例的一種恆等變形
• 舉例：合比定理、分比定理、等比定理等

基本介紹

誘導比例是比例的一種恆等變形，對於一個已知比例的一些項施行若干運算而得出一些新比例，稱為已知比例的誘導比例。從已知比例a/b=c/d可得下列誘導比例：

1.第一個比的兩項之和(或差)比其後項，等於第二個比的兩項之和(或差)比其後項，即

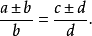
2.第一個比的兩項之和(或差)比其前項，等於第二個比的兩項之和(或差)比其前項，即

3.第一個比的兩項之和比它們的差，等於第二個比的兩項之和比它們的差，這稱為合分比定理，即

4.從上述性質1，2和3再利用更比定理和反比定理，尚可得出下列誘導比例：

相關介紹

在所有的比例中，它的兩個外項的積等於兩個內項的積。這叫做比例的基本性質。用式子表示這一性質，就是：

如果 (a、b、c、d都不等於零)

那么ad= bc。

證明用bd去乘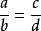 的兩邊，即

所以，ad= bc。

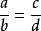
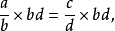
下面分析一下ad=bc的誘導比例。

由此性質可以推出：

如果兩個數的乘積等於另外兩個數的乘積，那么這四個數成比例(也就是可以組成比例)。用式子表示，就是

如果ad=bc，那么。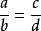

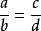
證明用bd去除ad=bc兩邊，即

得

我們還可以分別用cd、ab、ac去除ad=bc兩邊，得到不同的比例：

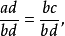
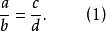
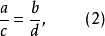
如果把(1)、(2)、(3)、(4)四個比例的左右兩邊對調，那么又可以得到四個比例：

由此可以看出，如果兩個數的積等於另外兩個數的積，那么這四個數就可以組成八個比例。這八個比例的形式不同，也就是各個數在比例中的位置不同。這八個比例叫做ad=bc的誘導比例。