試位法

試位法是計算作為一個方程的根的未知量的一種方法，是先做出一個或者一些估計，再從這個或者這些估計出發並根據未知量的性質求出代求的未知量。試位法類似於二分法，也是將含根區間逐漸縮小，但它並不是單一的二分區間，而是利用區間兩個端點的線性插值來求一個近似根。

基本介紹

• 中文名：試位法
• 外文名：False Position
• 作用：計算方程根的一種方法
• 套用學科：數學
• 別稱：線性插值方法

背景

試位法（False Position）（in Latin,regula falsi)試位法是在計算機工具非常落後的條件下人們為了改進二分法而得到的一個方法。由於算法原理有其合理性的一面，所以在如今的計算機條件下，在一些特定條件下還可繼續發揮作用。

與二分法類似，假設 在區間 上連續且滿足 。二分法中使用 的中點進行下一次疊代，儘管這種強力的算法極其有效，但卻是相當低效的。二分法的一個缺點是：在等分區間 的過程中，沒有考慮函式值 和 的大小。比如，如果 比 更加接近0，那么根很可能更加接近 而不是 。

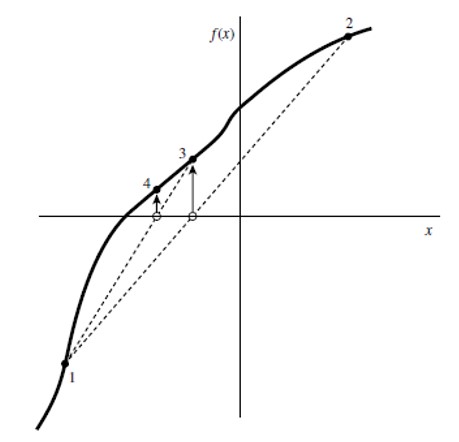
一個可行的方法，如右圖中表示的，通過一條直線連線 和 。這條直線和x軸的交點表示改進根的估計值。因為在這個根的求解中用直線代替了曲線，所以這個算法稱為“試位法”，或者拉丁文稱為“regula falsi”，該算法也稱為“線性插值方法”。

計算方法

根據相似三角形，直線與x軸的交點估計值如下式：

解得

該公式即為試位公式， 的值用該公式計算， 作為第一次近似根，將區間 分成 和 兩個區間，如果 ，則根在區間 中，否則根在區間 中，用新得到的根區間重複上述步驟，直到近似根 滿足一定的要求。

試位法的缺點與改進

可以預期，如果 在 上的圖像非常接近的一條直線，那么試位法的效果會明顯優於二分法。然而實際情況並非總是如此，有時候也會不盡人意。如圖，如果區間 的長度比較大，曲線 在 內拐彎比較大（一階導數值突然急劇增長），在這種情況下，試位法的效果一下子變得非常糟糕，反而不如二分法。

試位法出現“不動點”

在右圖所示的情況下，試位法出現了一個端點總是不動的情形，因此近似根只從一端收斂域精確根，我們並不希望這種情況的出現，因為它減慢了收斂速度。尤其當初始區間很大或函式在區間內偏離線性近似很遠時收斂更慢。為了消除這種情況下的負面影響，可以對試位法做相應改進。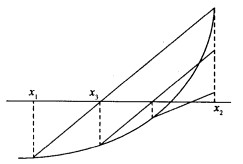

改進的試位法

在改進的試位法中，如果一個端點重複兩次或更多次作為新的含根區間的端點（稱為不動點），則我們將這個點的函式值乘以一個大於0小於1的常數因子w，比如可以取w=0.5，其目的是為了使線性插值的根更接近於精確根。這種改進真正體現了“試位”的思想。