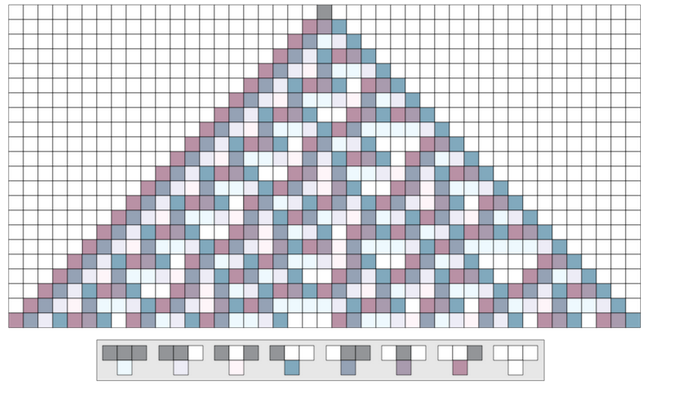
規則集 在Wolfram的所有基本細胞自動機中,考慮了具有僅兩種狀態的無限一維細胞自動機細胞陣列,每個細胞處於一些初始狀態。 在離散的時間間隔,每個細胞基於其當前狀態和其兩個鄰居的狀態自發地改變狀態。 對於規則30,管理自動機下一個狀態的規則集是:
當前模式
111
110
101
100
011
010
001
000
新狀態
如圖1所示顯示了創建的模式,單元格基於其鄰域的先前狀態而著色。 較暗的顏色代表“1”,較淺的顏色代表“0”。 時間沿垂直軸向下增加。
圖1
結構和性質 以下模式從單個單元格中的初始狀態出現,狀態1(顯示為黑色)被狀態為0(白色)的單元包圍。
規則30細胞自動機
這裡,縱軸表示時間,圖像的任何水平橫截面表示陣列中在圖案演變中的特定點處的所有單元的狀態。在這種結構中存在幾個圖案,例如白色三角形的頻繁出現和左側明確的條紋圖案; 但整個結構沒有明顯的模式。生成n的黑色單元的數量由序列給出。
1,3,3,6,4,9,5,12,7,12,11,14,12,19,13,22,15,19 ......
並且大約是n。
混沌 Wolfram將他對規則30的分類基於混沌主要基於其視覺外觀,但後來證明它符合Devaney和Knudson提出的更嚴格的混沌定義。特別是,根據Devaney的標準,規則30顯示了對初始條件的敏感依賴性(兩個初始配置僅在少數單元中快速分離),根據Cantor拓撲,其周期配置在所有配置的空間中都是密集的在配置空間(存在具有任何有限模式的單元的周期性配置),並且它是混合的(對於任何兩個有限的單元模式,存在包含一個模式的配置,最終導致包含其他模式的配置)。根據Knudson的標準,它顯示出敏感的依賴性並且存在密集的軌道(最初的配置最終顯示任何有限的細胞模式)。規則的混沌行為的這兩個特徵都來自規則30的更簡單且易於驗證的屬性:它是置換的,意味著如果兩個配置C和D在位置i處的單個單元的狀態不同,則在單步驟新配置將在單元格i+1處不同。
套用 隨機數生成 儘管沒有任何可以合理地被認為是隨機輸入的東西,但規則30產生看似隨機性。 Stephen Wolfram建議使用其中心列作為偽隨機數發生器(PRNG);它通過了許多標準的隨機性測試,Wolfram以前在Mathematica產品中使用這個規則來創建隨機整數。雖然規則30在許多輸入模式上產生隨機性,但是也存在導致重複模式的無限數量的輸入模式。這種模式的簡單示例是僅由零組成的輸入模式。由Matthew Cook發現的一個不那么簡單的例子是任何輸入模式,包括模式'00001000111000'的無限重複,重複可選地由六個分開。 Frans Faase發現了更多這樣的模式。請參閱重複規則30模式。
Sipper和Tomassini已經證明,作為隨機數生成器,與其他基於元胞自動機的生成器相比,當套用於所有規則列時,規則30在卡方檢驗中表現出較差的行為。作者還表達了他們的擔憂,“規則30 CA獲得的相對較低的結果可能是由於我們考慮了並行生成的N個隨機序列,而不是Wolfram認為的單個序列。
裝飾 劍橋北火車站裝飾有建築鑲板,展示規則30的演變(或等效於黑白逆轉,規則135)。 該設計被其建築師描述為靈感來自Conway的生命遊戲,這是劍橋數學家John Horton Conway研究的另一種細胞自動機,但實際上並非基於生命。