基本介紹
簡要實現方法,具體實現過程,比賽過程第四步,比賽過程第五步,名詞解釋,瑞士制的特點,疑問解答,模擬比賽過程,賽制變種,加速配位,麥克馬洪制,康拉德制,萬智牌賽制,拼字比賽賽制,優缺點分析,
簡要實現方法
隨機公平地編排第一輪比賽（一般由抽籤決定），接著開始比賽，當某一輪比賽結束後，可以得到所有比賽選手的總積分，根據這個總積分的高低，把比賽選手的由高到低排序，接著是高分比高分，低分比低分，上一輪比過的下一輪就不會相遇，如此循環，直到所有輪次結束。
備註： 第一輪比賽結束後：
總積分 = 第一輪積分
第二輪比賽結束後：
總積分 = 第一輪積分 + 第二輪積分
如此類推。
具體實現過程
（備註：由軟體自動編排，基本不需要手工計算）
根據報名比賽的人數，決定比賽的輪次。
人數少，輪次則少，人數越多，輪次越多。
輪次取經過N輪比賽後，能夠得出名次的最小輪次。
通常用以下公式確定具體輪次：2^（x-1)≤ y ≤2^x （x 代表輪次 ，y 代表參賽人數）
例如：有60人參加比賽，需要比賽6輪，即可以得出所有選手的具體名次。
以下假設：
有 A B C D E F G H 共8個人參加比賽，比賽3輪。
（下棋，分為：贏 輸 和 三種情況，假定贏的積1分，輸的積0分，和棋積0.5分）
比賽過程第一步
確定比賽名稱和輪次（確定具體輪次的方法見上面的公式），然後根據編號的先後順序，輸入所有參賽選手的信息。（備註：事先要通過抽籤，確定每一位參賽選手的編號）。
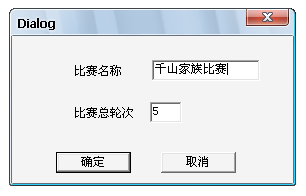比賽名稱和輪次
比賽過程第二步
由軟體自動化編排第一輪比賽的對陣表，由於事先的抽取編號具有隨機性，因此顯得公平。
由第一輪比賽對陣表可以看出：第一輪是 A對B ，C對D ，E對F ，G對H
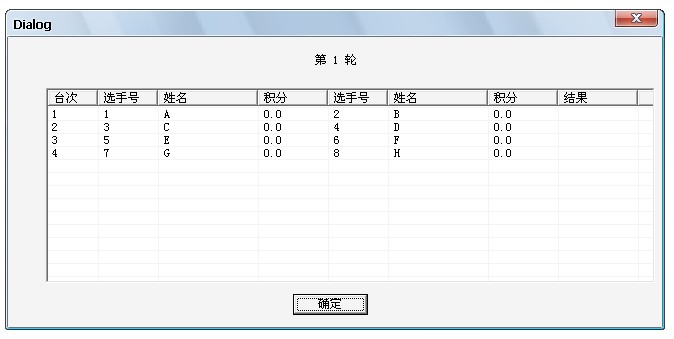
假定第一輪比賽結果是 A C E 贏 ，B D F 輸，G H 和棋。
那么，在第一輪比賽中 A C E 的積分是1分 ，B D F積分是0分，G H 的積分是0.5分
總積分是， A C E 的積分是1分 ，B D F積分是0分，G H 的積分是0.5分
（總積分 = 第一輪積分）
（注意：前三組都是分了勝負，只有最後一組是和棋，在第二輪比賽中，和棋的雙方，即使是積分最相近，也不會相遇）
比賽過程第三步
根據第一輪的成績，編排出來第二輪的比賽對陣表:
從第二輪對陣表可以看出第一輪成績。
第二輪對陣表
第二輪對陣表（可以看出來，由於G和H在第一輪已經比賽過，所以即使G和H在第一輪比賽中和棋，積分最相近，在第二輪比賽也不會相遇）
由上圖可以看出，第二輪比賽是 E對C H對A F對G D對B
假定第二輪比賽是 E贏C輸 ； H A和棋 ； F 輸G贏 ；D贏B輸
那么，在第二輪比賽中， E G D的積分是1分 ，C F B積分是0分， H A的積分是0.5分
總積分是（由高到低排序）：（總積分 = 第一輪積分 + 第二輪積分）
E 2.0分 A 1.5分 G 1.5分 C 1.0分 D 1.0分 H 1.0分 B 0分 F 0分
比賽過程第四步
第二輪比賽結束後，根據總積分，編排第三輪比賽，以下是第三比賽對陣表。
由第三輪比賽對陣表可以看出
第三輪對陣表
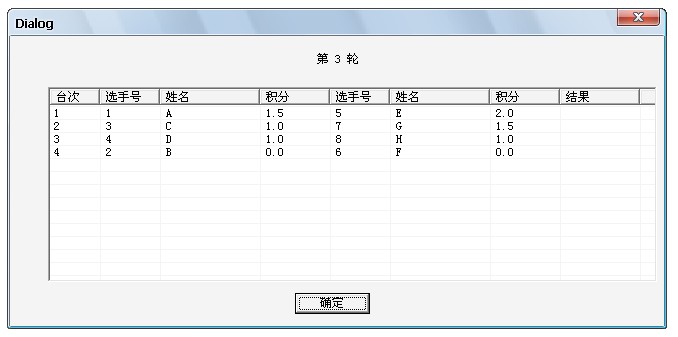第三輪對陣表第三輪比賽是 A 對E C 對G D 對H B對F
（注意：A 和 G 都是1.5分，但是沒有互相比賽，因為：假如A對G，那么E就要對上C，而 E是2.0分 ，C是1.0分，E和C的積分不相近，所以不能E對C ）
第三輪比賽結束後，根據成績編排第四輪比賽，
第四輪比賽結束後，根據成績編排第五輪比賽，
如此類推，直到比賽全部結束。
比賽過程第五步
所有輪次結束後，由軟體計算總成績，把所有選手的成績由高到低全部輸出，得出名次。其中每一位選手都有三個參數：大分、小分、累進分。
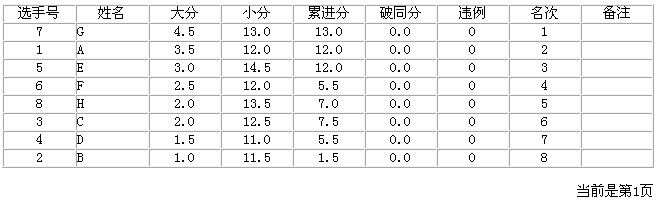具體積分和名次名詞解釋
大分：各參賽選手的最後總得分之和；
小分：各選手的所遇到過的對手的大分之和（意味著此選手對手的實力）；
累進分：各選手每一輪的得分之和。
例如：某位棋手第一輪勝得1分，累計1分；第二輪勝得1分，累計2分；第三輪和得0.5分，累計2.5分，第四輪勝累計3.5分。
這位棋手4輪比賽的分數：
大分：1+1+0.5+1=3.5
小分：這位棋手在4輪比賽里的對手的大分之和
累計分：1+2+2.5+3.5=9
大分越高，名次越靠前；當大分相同時，比較小分，小分越高，名次越靠前。
（備註：也有比賽採用累進分作為名次的判斷標準，累進分越高，名次越靠前。
採用累進分的優點是：決定棋手名次的命運由自己掌握，不受客觀因素擺布。實力強者早贏早拿分，不但積分高，累進分也高，名次自然也高。）
瑞士制的特點
第一：下一輪比賽的對陣表需由上一輪的比賽成績來推出，也就是說，編排第二輪對陣表，需要知道第一輪的成績，編排第三輪對陣表，就需要知道第二輪的成績，如此類推。
第二：相對高分VS相對高分，相對低分VS相對低分，保證了比賽的平衡（方法見實現過程的第三步）。
第三：瑞士制並不淘汰選手，所有選手都資格參與全部輪次的比賽，符合棋類比賽友誼第一，比賽第二的原則。
第四：每一輪比賽可以只由一場比賽構成，一場定勝負，而不採用三局兩勝制等的制度，節省了大量的時間。因為三局兩勝制、五局三勝制、七局四勝制等是配套淘汰制使用的，目的是為了消除一定的偶然性，保證實力更強者晉級。而瑞士制並不淘汰選手出局，假如實力更強者在某輪比賽中偶然地輸給了實力較弱者，實力更強者的名次下跌，實力較弱者的名次上升，那么在下一輪比賽中，實力更強者會遇到相對較弱的對手，使其名次重新靠前，而實力較弱者則會因為上一輪偶然地戰勝了實力更強者而遇到更加強的對手，使其名次重新靠後。如此經過多輪比賽，基本消除了偶然性的影響，名次排列均衡，能夠體現出選手的真實水平。
疑問解答
瑞士制公平嗎？
答：瑞士制是公平的，是在循環制和淘汰制的基礎上制定的。
每一輪的比賽編排，都是根據總積分進行編排的，而總積分就是前面所有輪次積分的總和，體現的是選手的實力。
也就是說，安排積分相近的兩個選手比賽（當前名次相近的選手比賽），就等於安排實力相近的兩個選手比賽，避免的強者對弱者的尷尬局面（避免了實力懸殊的出現）。
（對總積分進行排序，就能得到名次，分高者名次靠前）
瑞士制消除了偶然性嗎？
答：瑞士制消除了偶然性。
因為瑞士制並不淘汰選手，所有選手都有資格參與全部輪次的比賽，選手假如實力更強者在某輪比賽中偶然地輸給了實力較弱者，實力更強者的名次就會下跌。（備註：總積分的排序，就是名次）
瑞士制可以配套3局2勝制等使用嗎？
答：當然可以，每一輪比賽設定為3局2勝就可以了。
但是不建議配套使用3局2勝制，因為瑞士制本身已經通過多輪比賽輪消除了偶然性（原理見瑞士制的特點四）。
瑞士制如何解決先後手問題
答：在比賽中，要儘量使棋手執黑棋（先手）與執白棋（後手）的次數相等，普遍採用的辦法是輪換使用黑白棋。但不管怎樣，絕不能出現一名棋手連續3輪執一種顏色的情況
由此可見，“瑞士制”是一種兼具循環賽和淘汰賽主要優點，但又避免此兩種比賽主要缺點的賽制，確是獨具一格。
模擬比賽過程
（軍棋）
假設有12 組參加比賽（網路比賽），進行3 天比賽（每天晚上的 7:30-10:50 ）。
比賽輪次為 6 輪 ，每一輪採用3盤2勝制，時間1.5小時。
每一輪比賽共需要下3 盤（如果2盤就分出勝負，則只需要下2盤）。
勝負的判定
在某一輪的3 場比賽中，如果勝出2盤，則判為贏，如果贏1盤+和棋2盤，也判斷為贏。
在某一輪的3 場比賽中，如果輸了2盤，則判為負，如果輸1盤+和棋2盤，也判斷為輸。
在某一輪的3 場比賽中，如果3盤都是和棋，則判為和，如果贏1盤+輸1盤+和1盤，也判斷為和。
在某一輪的比賽中，選手遲到15分鐘或以上的，則直接判為負。
所有輪次：
勝 記 1分
輸 記 0分
和 記 0.5分
注意：這個積分是每一輪的積分，而不是每一盤的。也就是說，下完3盤後，對應輪次就會結束，得到輪次的積分。
總體概述
比賽時間共為3天，每一輪比賽3盤，時間為1.5小時，下完每一輪，休息時間為15分鐘。
（備註：第一輪比賽的對陣表是隨機生成的，具有公平性、規範性。）
詳細時間：
第一天
7:30-9:00 進行 第一輪比賽。
9:00-9:10 根據第一輪比賽成績，編排第二輪比賽的對陣表。
9:15-9:20 根據第二輪比賽的對陣表，選手開始找到相應座位，坐好，準備比賽。
9:20-10:50 進行 第二輪比賽。
10:50 - 睡覺前 編排好第三輪比賽對陣表（只需要30 秒）。裁判員會議，總結等。
第二天
7:30-9:00 進行 第三輪比賽。
9:00-9:10 根據第三輪比賽成績，編排第四輪比賽的對陣表。
9:15-9:20 根據第四輪比賽的對陣表，選手開始找到相應座位，坐好，準備比賽。
9:20-10:50 進行 第四輪比賽。
10:50 - 睡覺前 編排好第五輪比賽對陣表（只需要30 秒）。裁判員會議，總結等。
第三天
7:30-9:00 進行 第五輪比賽。
9:00-9:10 根據第五輪比賽成績，編排第六輪比賽的對陣表。
9:15-9:20 根據第六輪比賽的對陣表，選手開始找到相應座位，坐好，準備比賽。
9:20-10:50 進行 第六輪比賽。
10:50 - 睡覺前 輸入第6輪比賽成績，並統計出總成績，得出最終排名，頒獎。
賽制變種
加速配位
加速配位常用於參賽者過多而輪次相對較少的比賽，是為了儘快減少全勝選手的數目（即在相對較少的輪次中決出優勝者），而使領先選手儘快相遇（即加速配位）的一種方法。
在前兩輪比賽中，選擇配位時上半區的選手自動加上1分配位分（此分數隻為幫助加速配位，並不計入成績）。實際的效果就是，在第一輪中，如果將選手按排名分成1、2、3、4個等級，那么第1等將對陣第2等，第3等對陣第4等。理想情況下，假設大家發揮正常，那么第1等和第3等的選手將勝出。在第二輪中，為上半區（此時為1等與3等）選手再加上一分配位分後進行配位，實際效果就相當於1等與1等比，2等與3等比，4等與4等比...兩輪過後，會有大約1/8的選手全勝，大大低於傳統瑞士制下全勝選手機率（1/4）。第二輪之後的輪次，則回到傳統的瑞士制，不再為上半區選手加配位分。
麥克馬洪制
麥克馬洪制(McMahon system)是一些歐洲圍棋俱樂部賽使用的特殊瑞士制。與普通瑞士制不同的是，選手按段位高低得到不同的初始積分，只有當所有選手都在同一段位的特殊情況時，才是標準的瑞士制。最後的總積分成為麥克馬洪分，這一名稱由貝爾實驗室的Lee McMahon最早用於他所在的圍棋俱樂部，故名。
康拉德制
康拉德制也是瑞士制的一個變種，主要用於某些輪次間隔較大跨時很長的比賽。為了方便參賽選手，不要求每輪都參加，最後排名只取每名選手最好的幾輪次來計算總分（如最好的5輪或7輪），選手可以在任意輪次加入或退出。這樣的賽制比較靈活，既可以吸引一些為冠軍而來的選手，也可以吸引一些沒有太多時間，只想臨時參與的選手。挪威的一些西洋棋俱樂部即採用這種賽制。
萬智牌賽制
萬智牌比賽採用一種特別的瑞士制計分法，勝者獲得3分，平局得1分，其它規則與普通瑞士制相同。有的萬智牌比賽也採用前8名再進行附加淘汰賽的辦法來決出冠軍。這個賽制的缺點是在倒數第二輪，如果4名全勝的選手相遇，他們可以選擇於賽前協定和局，因為這樣也可以保證他們進入前8名的附加淘汰賽。
拼字比賽賽制
在拼字比賽(scrabble)中常使用的一種瑞士制變種，即選手們先按4個一組進行循環賽，然後在循環賽積分的基礎上進行瑞士制，也叫做波特蘭瑞士制(Portland Swiss)。實際比賽時，因為配位過程往往時間很長，為了加速比賽進程，組織者常常只取循環賽中的倒數第二輪積分，而不是最後一輪積分來進行瑞士制配位。
北美及加拿大拼字比賽中還採用另外一種瑞士制變種，先計算每名選手是否仍有可能獲得冠軍，在所有這些可能的冠軍者多者中，選擇第一名與最後一名對陣並以此類推；而在已經退出冠軍爭奪行列的選手中，按照傳統的瑞士制配位。
優缺點分析
要無爭議地確定一次大賽的冠軍（或最後一名），理論上需要與淘汰賽所需的相同輪次，即參賽選手數目取2的對數。如8名選手需要3輪比賽確定冠軍，16名選手需要4輪比賽確定冠軍。但有時候比賽輪次比理論上少，就會出現所有輪次結束後，有多於一名選手全勝的情況。
瑞士制相對於淘汰制固有的優勢就是無須淘汰任何參賽者。選手在參賽前就可以確定不管發揮如何，自己都確保可以參加所有輪次的比賽而不用擔心被提前淘汰。最差的情況無非是當有奇數名選手參加時，會有一輪沒有比賽（即輪空），但仍可以確保拿到1分。一名選手最多只會有一輪輪空。瑞士制並非像淘汰賽一樣，會把懸念保留到最後一場比賽，有的時候某名選手的領先優勢過大，提前一輪甚至幾輪就可以確保冠軍。一個常見的彌補辦法就是先進行瑞士制，然後在前幾名選手中再進行淘汰賽決出冠軍。
瑞士制相對於循環賽的優勢在於，當參賽選手很多時，無需進行過多輪比賽。
瑞士制的一個缺點就是除了最後的冠軍與最後一名，取決於不同的小分記法或破同分法，中間選手的排名可能比較粗略並可能出現隨機或抽籤的情況。
