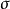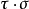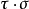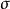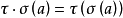複合映射是映射g和f構成的複合映射。映射f和g構成複合映射的條件是:g的值域必須包含在f的定義域內,否則,不能構成複合映射。
基本介紹
- 中文名:複合映射
- 外文名:composite mapping
- 類型:名詞
- 領域:數學
- 相關:映射g和f構成的複合映射
- 套用學科:數學術語
概念,基本定理,
概念
對二元關係可以進行複合運算和逆運算,映射也是一種二元關係,按照關係的複合運算可以對複合映射給出下面定義。
定義:設映射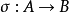 ,
,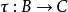 ,則
,則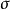 與
與 的複合映射,是一個從
的複合映射,是一個從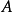 到
到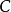 的映射,記作
的映射,記作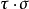 ,簡記作
,簡記作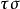 ,即
,即
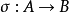
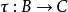
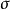

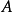
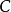
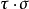
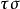

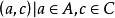


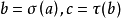
基本定理
定理1:設映射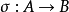 ,
,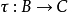 ,
,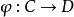 ,則
,則
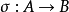
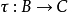
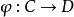
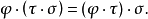
定理1的證明:由映射與複合映射的定義可知,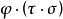 與
與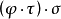 都是
都是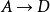 的複合映射。
的複合映射。
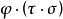
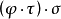
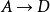
對於任意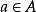 ,設
,設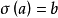 ,
,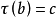 ,
,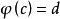 ,其中
,其中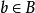 ,
,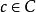 ,
,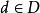 ,則
,則
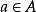
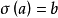
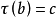
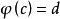
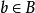
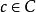
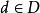
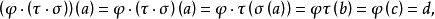
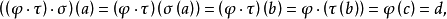

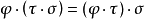
定理2:設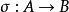 ,
,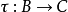 ,
,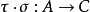 ,則
,則
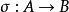
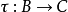
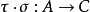
(1)若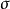 與
與 都是滿射,則
都是滿射,則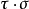 也是滿射;
也是滿射;
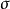

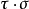
(2)若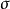 與
與 都是單射,則
都是單射,則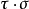 也是單射;
也是單射;
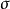

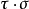
(3)若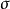 與
與 都是雙射,則
都是雙射,則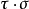 也是雙射。
也是雙射。
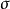

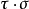
定理2的證明:(1)設任意 ,由於映射
,由於映射 是滿射,所以存在某個
是滿射,所以存在某個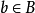 ,使得
,使得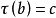 。又因為映射
。又因為映射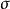 也是滿射,也必有某個
也是滿射,也必有某個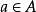 ,使得
,使得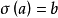 ,於是
,於是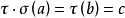 ,因此
,因此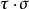 是滿射。
是滿射。


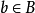
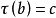
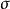
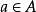
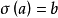
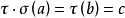
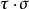
(2)設任意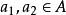 ,且
,且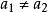 ,由於映射
,由於映射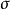 是單射,所以
是單射,所以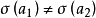 ,又由於映射
,又由於映射 也是單射,所以
也是單射,所以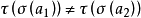 。因此,由
。因此,由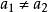 可得
可得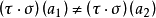 ,故
,故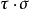 是單射。
是單射。
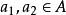
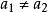
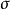
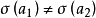

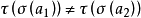
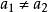
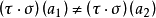
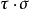
(3)由於映射 和
和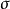 都是雙射,由(1)和(2),可以得出
都是雙射,由(1)和(2),可以得出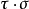 既是滿射又是單射,所以
既是滿射又是單射,所以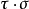 也是雙射。證畢。
也是雙射。證畢。