基本介紹
- 中文名:表兄弟素數
- 外文名:Cousin primes
- 別名:相差4的孿生素數
概念,公式,孿生素數猜想,
概念
一千以內的表兄弟素數(OEIS中的數列A023200及A046132) 如下:
(3, 7), (7, 11), (13, 17), (19, 23), (37, 41), (43, 47), (67, 71), (79, 83), (97, 101), (103, 107), (109, 113), (127, 131), (163, 167), (193, 197), (223, 227), (229, 233), (277, 281), (307, 311), (313, 317), (349, 353), (379, 383), (397, 401), (439, 443), (457, 461), (463,467), (487, 491), (499, 503), (613, 617), (643, 647), (673, 677), (739, 743), (757, 761), (769, 773), (823, 827), (853, 857), (859, 863), (877, 881), (883, 887), (907, 911), (937, 941), (967, 971)
公式
表兄弟素數,即相差4的孿生素數
利用素數判定法則,【若自然數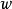 與
與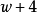 都不能被不大於
都不能被不大於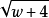 任何素數整除,則
任何素數整除,則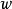 與
與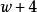 是一對素數。這是因為”若自然數
是一對素數。這是因為”若自然數 是一個素數,若且唯若它不能被不大於
是一個素數,若且唯若它不能被不大於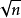 任何素數整除。
任何素數整除。
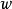
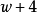
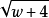
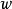
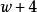

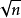
我們可以把上面的漢字內容等價轉換成為英語字母表示 成為公式:
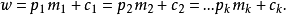
....(1)
其中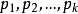 表示前面k個順序素數2,3,5,....。
表示前面k個順序素數2,3,5,....。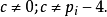 。
。
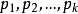
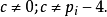
這樣解得的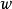 ,若
,若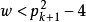 ,則
,則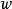 與
與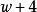 是一對素數。
是一對素數。
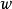
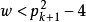
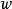
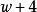
我們可以把(1)式內容等價轉換成為同餘式組表示:

由於(2)式的模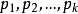 兩兩互素,根據孫子定理(中國剩餘定理)知,對於給定的
兩兩互素,根據孫子定理(中國剩餘定理)知,對於給定的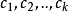 ,
,
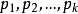
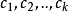
(2)式在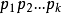 範圍內有唯一解。
範圍內有唯一解。
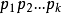
範例
例如:
k=1時,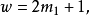 ,解得=3。
,解得=3。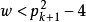 ,即
,即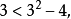 ,得知3與3+4是相差4的表兄弟素數。求得了(3,
,得知3與3+4是相差4的表兄弟素數。求得了(3, )區間的全部相差4的表兄弟素數。
)區間的全部相差4的表兄弟素數。
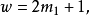
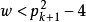
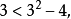

k=2時,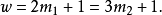 ,解得=13,19;
,解得=13,19;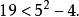 。得知13與13+4,19與19+4都是相差4的孿生素數。求得了(5,
。得知13與13+4,19與19+4都是相差4的孿生素數。求得了(5,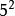 )區間的全部相差4的孿生素數。
)區間的全部相差4的孿生素數。
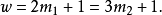
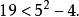
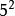
k=3 | 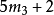 | 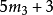 | 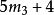 |
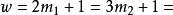 | 37 | 13 和 43 | 19 |
求得了(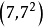 )區間的全部相差4的孿生素數。即:37與37+4,,43與43+4,....,都是相差4的表兄弟素數。
)區間的全部相差4的孿生素數。即:37與37+4,,43與43+4,....,都是相差4的表兄弟素數。
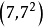
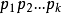
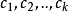
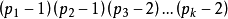
個解。

